��Ŀ����
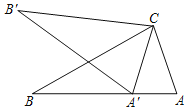
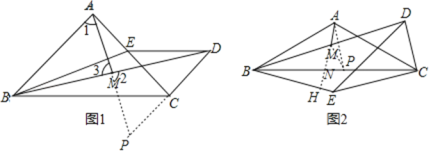
����Ŀ����ABC�͡�CDE���Ե�CΪ������������������Σ�

��1����ͼ1����AB��AC��CD��CE����BAC����DCE��90��ʱ������BD��ȡBD���е�M������AM��̽��AM��BE֮���������ϵ����֤����Ľ��ۣ�
��2����ͼ2����AB��AC����BAC��120�㣬��CDE��60�㣬��DCE��90��ʱ������BD��ȡBD���е�M������AM��̽��AM��BE֮��Ĺ�ϵ����֤����Ľ��ۣ�
���𰸡���1��BE��2AM����2��AM��BE����BE��2![]() AM��
AM��
��������
��1���ӳ�AM��DC���ڵ�P������BD���е�M����ȫ�ȵ������Ρ�ABM�ա�PDM���ó�AP��2AM����֤��ABE�ա�ACP��֤��BE��AP��2AM��
��2��ȡBC���е�P������MP��AP���ӳ�AM��BC�ڵ�N����BE�ڵ�H,���������ε���λ�ߵõ�CD=2MP,������ֱ�������Ρ�DCE֤��![]() ��2
��2![]() �����õ��������ε�����ͬ���õ�
�����õ��������ε�����ͬ���õ�![]() ��2
��2![]() ���ɴ˵õ�
���ɴ˵õ�![]() ��
��![]() ����֤��APM�ס�BCE�õ�
����֤��APM�ס�BCE�õ�![]() ��
��![]() ��2
��2![]() ����BE��2
����BE��2![]() AM���ٸ��ݵȽǵĴ�����ϵ�õ���EBC+��BNH��90������AHB��90�����õ�AM��BE.
AM���ٸ��ݵȽǵĴ�����ϵ�õ���EBC+��BNH��90������AHB��90�����õ�AM��BE.
��1��BE��2AM��
֤������ͼ1���ӳ�AM��DC���ڵ�P��
�ߡ�BAC����DCE��90�㣬��AB��CD��
���1����P��
��M��BD�е㣬
��BM��DM��
�ߡ�3����2��
���ABM�ա�PDM��AAS����
��AB��PD��AC��AM��PM��
��AP��2AM��
��CD��CE��
��AC��CE��DP��CD����AE��CP��
�ߡ�ACP��180�㩁��DCE��90�㣽��BAC��
AB��AC��
���ABE�ա�ACP��SAS��
��BE��AP��2AM��
��2��AM��BE����BE��2![]() AM��
AM��
֤������ͼ2��ȡBC���е�P������MP��AP���ӳ�AM��BC�ڵ�N����BE��H��
��M��BD�е㣬
��MP��CD��CD��2MP��
��Rt��DCE�У��ߡ�CDE��60�㣬��DCE��90�㣬
���DEC��30�㣬
��DE��2CD��
���ݹ��ɶ�������EC��![]() CD��
CD��
��![]() ��2
��2![]() ��
��
��AB��AC��P��BC�е㣬
��AP��BC��BC��2BP����BAP����CAP��
�ߡ�BAC��120�㣬
���BAP��60�㣮
ͬ����BP��![]() AP��
AP��
��![]() ��2
��2![]() ��
��
��![]() ��
��![]() ��
��
��MP��CD���MPB����BCD��
�ߡ�BPA����DCE��90�㣮
���BPA����MPB����DCE����BCD��
���MPA����ECB��
���APM�ס�BCE��
��![]() ��
��![]() ��2
��2![]() ����BE��2
����BE��2![]() AM��
AM��
��PAM����EBC��
�ߡ�PAM+��ANP��90�㣬��ANP����BNH��
���EBC+��BNH��90�㣮
���AHB��90�㣮
��AM��BE��
����AM��BE֮��Ĺ�ϵΪ��AM��BE��BE��2![]() AM��
AM��

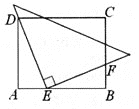
����Ŀ��ɽ��ʡʵ����ѧ�����廪��ѧ�Ƽ�һ��ѧ�������ݹ涨���Ƽ����������ɱ��꼶200��ѧ������ͶƱ��ÿ��ֻ���Ƽ�һ�ˣ�������ȨƱ����ѡ����Ʊ�����ļס��ҡ������ˣ�ͶƱ���ͳ����ͼ1��
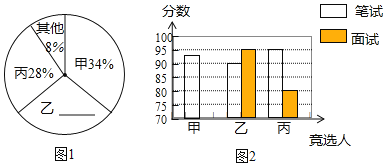
��Σ���������ѡ�˽����˱��Ժ�����������ԣ�����ɼ������ʾ��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 92 | 90 | 95 |
���� | 85 | 95 | 80 |
ͼ2��ijͬѧ�����ϱ����Ƶ�һ������ȫ������ͼ���������������Ϣ����������⣺
��1����ȫͼ1��ͼ2��
��2�������ÿ����ѡ�˵ĵ�Ʊ����
��3����ÿ����ѡ�˵�һƱ��1�֣�ͶƱ�����ԡ���������÷ְ���2��5��3�ı�ȷ��������������ѡ�˵�ƽ���ɼ����ɼ��ߵĽ���¼ȡ��Ӧ��¼ȡ˭��
��4����ѧУ��������������ѡ�������ѡ�����μ��廪��ѧ����Ӫ������ұ�ѡ�еĸ��ʣ���Ҫ���б�����״ͼ��