题目内容
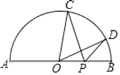
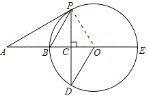
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,
∠AOD=∠APC.

(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明详见解析;(2)![]()
【解析】
(1)连接OP,证明OP⊥AP,利用等腰三角形的性质和直角三角形的性质证明即可;(2)根据扇形POD面积减去△OPD的面积即为阴影部分的面积,求出相关数据代入计算.
(1)证明:连结OP,∵PD⊥BE,如图.
∴∠OCD=90°,
∴∠ODC+∠COD=90°,
∵OD=OP,
∴∠ODC=∠OPC,
∵∠COD=∠APC,
∴∠OPC+∠APC=90°,
∴∠APO=90°,即AP⊥PO,
∵P在⊙O上,∴AP是⊙O的切线.
(2)在Rt△APO中,tan∠AOP=![]() ,
,
∴∠AOP=60°,∴∠OPC=30°,
∴OC=2,∴PC=![]() ,
,
∴PD=![]() ,
,
∵OD=OP,OB⊥PD,
∴∠POB=∠COD=60°,
∴∠POD=120°,
∴阴影部分面积为:![]() .
.

练习册系列答案
相关题目