题目内容
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
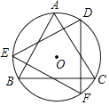
A.150°B.135°C.120°D.105°
【答案】C
【解析】
连结OA、OE、OD、AE、AD,根据旋转的性质得∠AOD=30°,再根据圆周角定理得∠AED=![]() ∠AOD=15°,然后根据等边三角形的性质得∠EFD=60°,则∠DOE=120°,求出∠AOE=∠DOE-∠AOD=90°,则∠ADE=45°,根据三角形内角和可求出∠EAD的度数.
∠AOD=15°,然后根据等边三角形的性质得∠EFD=60°,则∠DOE=120°,求出∠AOE=∠DOE-∠AOD=90°,则∠ADE=45°,根据三角形内角和可求出∠EAD的度数.
如图,连结OA、OE、OD、AE、AD,
∵△ABC绕点O顺时针旋转30°得到△DEF,
∴∠AOD=30°,
∴∠AED=![]() ∠AOD=15°,
∠AOD=15°,
∵△DEF为等边三角形,
∴∠EFD=60°,
∴∠DOE=2∠EFD=120°,
∴∠AOE=∠DOE-∠AOD=120°-30°=90°,
∴∠ADE=![]() ∠AOE=45°,
∠AOE=45°,
∴∠EAD=180°-∠AED-∠ADE=180°-15°-45°=120°.
故选:C.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目