题目内容
【题目】某运动专营店为某厂家代销一款学生足球比赛训练鞋（这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理），当每双鞋的售价为260元时，月销售量为63双为提高经营利润，该专营店准备采取降价的方式进行促销，经市场调查发现，每月的销售量y（双）与销售单价x（元/双）之间的函数关系如图所示综合考虑各种因素，每售出双鞋需支付厂家其他费用150元.
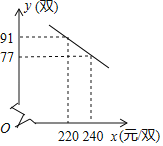
（1）求出y与x之间的函数关系式；
（2）该运动专营店要获取最大的月利润，售价应定为每双多少元？并说明理由．
（3）2019年3月底，该专营店老板清点了一下仓库，发现该款学生足球比赛训练鞋库存650双，若根据（2）中获得最大月利润的方式进行销售，12月底能否销售完这批学生足球比赛训练鞋？请说明理由．
【答案】（1）
；（2）该运动专营店要获取最大的月利润，售价应定为每双250元，见解析；（3）12月底不能售完，见解析.
【解析】
（1）利用待定系数法求解可得；
（2）根据“总利润＝单件利润×销售量”列出函数解析式，并配方成顶点式即可得出最大值；
（3）求出在（2）中情况下，即x＝250时的销售量，据此求得的总销售量，比较即可得出答案．
解：（1）设y与x的函数关系式为y＝kx+b，
将（220，91）、（240，77）代入，
得：
，
解得：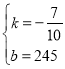
，
∴y与x的函数关系式为y＝﹣
x+245；
（2）设月利润为w，
则w＝（x﹣150）y
＝（x﹣150）（﹣x+245）
＝﹣（x﹣250）2+7000，
∴当x＝250时，w取得最大值，最大值为7000；
故该运动专营店要获取最大的月利润，售价应定为每双250元；
（3）由（2）知，当获得最大利润时，定价为250元/双，
则每月的销售量为y＝﹣×250+245＝70，
∴总销售量为70×（12﹣3）＝630，
∵630＜650，
∴12月底不能售完．
故答案为：（1） ；（2）该运动专营店要获取最大的月利润，售价应定为每双250元，见解析；（3）12月底不能售完，见解析.
