题目内容
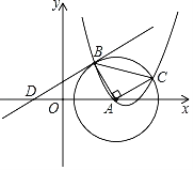
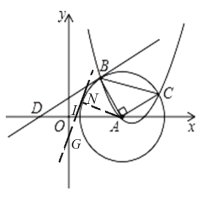
【题目】如图,已知的圆心为点![]() ,抛物线y=ax2﹣
,抛物线y=ax2﹣![]() x+c过点A,与
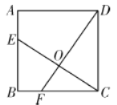
x+c过点A,与![]() 交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
(1)求B、C点坐标和抛物线的解析式;
(2)直线y=kx+1经过点B,与x轴交于点D.点E(与点D不重合)在该直线上,且AD=AE,请判断点E是否在此抛物线上,并说明理由;
(3)如果直线y=k1x﹣1与⊙A相切,请直接写出满足此条件的直线解析式.
【答案】(1)点B、C的坐标分别为(2,2)、(5,1),![]() ;(2)点E在抛物线上,理由见解析;(3)
;(2)点E在抛物线上,理由见解析;(3)![]() 或y=2x﹣1.
或y=2x﹣1.
【解析】
(1)根据题意,作出合适的辅助线,然后根据全等三角形的性质和判定可以得到点B和点C的坐标,然后将点B和C的坐标代入抛物线解析式,即可得到答案;
(2)根据(1)中的抛物线的解析式可以得到点D的坐标,从而可以求得直线BD的解析式,然后根据点E(与点D不重合)在该直线上,且AD=AE,即可得到点E的坐标,然后将点E的横坐标代入抛物线解析式,即可得到相应的纵坐标,即可判断点E是否在抛物线上;
(3)根据题意,画出相应的辅助线,然后利用分类讨论的方法可以求出满足条件的直线解析式.
解:(1)过点B、C分别作x轴的垂线交于点R、S,![]()
![]()
![]() ∠BAR+∠RBA=90°,∠BAR+∠CAS=90°,
∠BAR+∠RBA=90°,∠BAR+∠CAS=90°,
∴∠RAB=∠SCA,
又∵AB=AC,
∴![]() (AAS),
(AAS),
∴AS=BR,AR=CS,
∵B、C两点的纵坐标分别是2、1,![]()
∴AS=BR=2,AR=CS=1,
![]()
故点B、C的坐标分别为(2,2)、(5,1),
将点B、C坐标代入抛物线y=ax2﹣![]() x+c,
x+c,
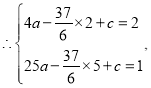
解得: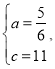
故抛物线的表达式为![]()
(2)∵直线y=kx+1经过点B(2,2),
∴2=2k+1,得![]()
即直线![]()
当y=0时,![]() 得x=﹣2,
得x=﹣2,
即点D的坐标为(﹣2,0),
∵点A、B、C、D的坐标分别为(3,0)、(2,2)、(5,1)、(﹣2,0),
∴![]() AD=5,
AD=5,
∵点E在直线BD上,
∴设E的坐标为![]() ,
,
∵AD=AE,
∴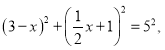
解得:x1=﹣2(舍去),x2=6,
∴点E(6,4),
当x=6时,![]()
∴点E在抛物线上;
(3)①当切点在x轴下方时,
设直线y=k1x﹣1与⊙A相切于点H,
直线与x轴、y轴分别交于点K、G(0,﹣1),连接GA,
∵AR=1,![]() ∠BRA=90°,点A(3,0),点G(0,﹣1),
∠BRA=90°,点A(3,0),点G(0,﹣1),
∴AB=![]() AG=
AG=![]()
∴AH=AB=![]()
∵∠AHK=∠KOG=90°,∠HKA=∠OKG,
∴![]() ,
,
∴![]() ,
,
即: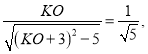
解得:KO=2或![]() (舍去),
(舍去),
经检验:![]() 符合题意,
符合题意,
∴点K的坐标为(﹣2,0),
把点K的坐标代入y=k1x﹣1,得
0=﹣2k1﹣1,得k1=![]() ,
,
∴直线的表达式为![]() ;
;
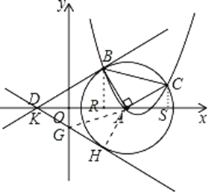
②当切点在x轴上方时,如图,切点为![]() ,
,
记![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]()
![]()
![]()
设![]() 则
则![]()
由勾股定理得:![]()
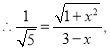
解得:![]() (舍去)
(舍去)
经检验:![]() 符合题意,
符合题意,
![]()
把![]() 代入y=k1x﹣1,
代入y=k1x﹣1,
![]()
![]()
![]() 此时切线为:
此时切线为:![]()
故满足条件的直线解析式为![]() 或y=2x﹣1.
或y=2x﹣1.

【题目】小明为探究函数![]() 的图象和性质,需要画出函数图象,列表如下:
的图象和性质,需要画出函数图象,列表如下:
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的![]() 的图象;
的图象;
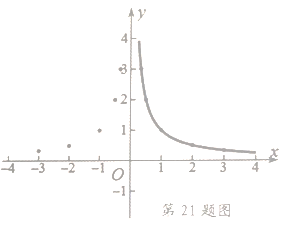
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数![]() 图象与直线
图象与直线![]() 的关系;
的关系;
①当![]() 时, 直线
时, 直线![]() 与函数
与函数![]() 在第一象限的图象有一个交点
在第一象限的图象有一个交点![]() ,则
,则![]() 的坐标是 ;
的坐标是 ;
②当![]() 为何值时,讨论函数
为何值时,讨论函数![]() 的图象与直线
的图象与直线![]() 的交点个数.
的交点个数.