题目内容
【题目】如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
(1)填空:若∠BAF=18°,则∠DAG=______°.
(2)证明:△AFC∽△AGD;
(3)若![]() =
=![]() ,请求出
,请求出![]() 的值.
的值.
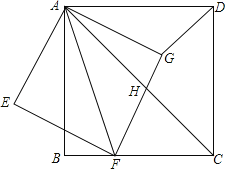
【答案】(1)27;(2)证明见解析;(3)![]() =
=![]() .
.
【解析】
(1)由四边形ABCD,AEFG是正方形,得到∠BAC=∠GAF=45°,于是得到∠BAF+∠FAC=∠FAC+∠GAC=45°,推出∠HAG=∠BAF=18°,由于∠DAG+∠GAH=∠DAC=45°,于是得到结论;
(2)由四边形ABCD,AEFG是正方形,推出![]() =
=![]() =
=![]() ,得
,得![]() =
=![]() ,由于∠DAG=∠CAF,得到△ADG∽△CAF,列比例式即可得到结果;
,由于∠DAG=∠CAF,得到△ADG∽△CAF,列比例式即可得到结果;
(3)设BF=k,CF=2k,则AB=BC=3k,根据勾股定理得到AF=![]() =
=![]() =
=![]() k,AC=
k,AC=![]() AB=3
AB=3![]() k,由于∠AFH=∠ACF,∠FAH=∠CAF,于是得到△AFH∽△ACF,得到比例式即可得到结论.
k,由于∠AFH=∠ACF,∠FAH=∠CAF,于是得到△AFH∽△ACF,得到比例式即可得到结论.
解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵![]() =
=![]() ,
,
设BF=k,
∴CF=2k,则AB=BC=3k,
∴AF=![]() =
=![]() =
=![]() k,AC=
k,AC=![]() AB=3
AB=3![]() k,
k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴![]() ,
,
∴![]() =
=![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目