题目内容
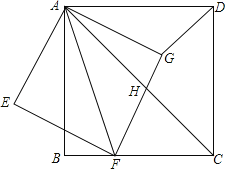
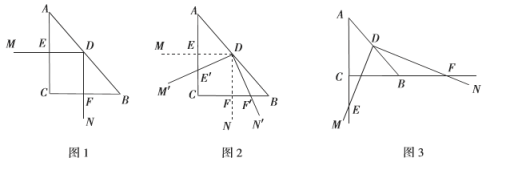
【题目】如图1,![]() 和
和![]() 是两个完全重合在一起的等腰直角三角形,
是两个完全重合在一起的等腰直角三角形,![]() .现将
.现将![]() 固定,将
固定,将![]() 绕点
绕点![]() 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() .
.
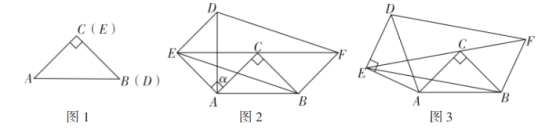
(1)如图2,当![]() 时,判断四边形
时,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)如图3,当![]() 时,(1)中的结论是否仍然成立?说明理由.
时,(1)中的结论是否仍然成立?说明理由.
【答案】(1)当![]() 时,四边形
时,四边形![]() 为平行四边形,理由见解析;(2)当
为平行四边形,理由见解析;(2)当![]() 时,(1)中的结论仍然成立,理由见解析
时,(1)中的结论仍然成立,理由见解析
【解析】
(1)利用已知得出![]() ,进而利用平行四边形的判定得出即可;
,进而利用平行四边形的判定得出即可;
(2)利用已知首先得出![]() ,进而求出
,进而求出![]() ,即可得出
,即可得出![]() ,进而得出答案;
,进而得出答案;
解:
(1)当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
理由如下:如图2所示.
∵由题可知,![]() 和
和![]() 是一对全等的等腰直角三角形,
是一对全等的等腰直角三角形,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴四边形![]() 为平行四边形.
为平行四边形.
(2)当![]() 时,(1)中的结论仍然成立.
时,(1)中的结论仍然成立.
理由如下:如图3所示.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .∵
.∵![]() ,∴
,∴![]() .
.
又∵![]() ,
,
∴四边形![]() 为平行四边形.
为平行四边形.

练习册系列答案
相关题目