题目内容
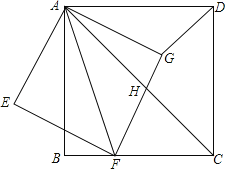
【题目】如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为_____(用含a、b的代数式表示).
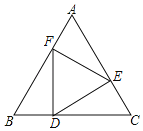
【答案】![]() (a﹣b).
(a﹣b).
【解析】
根据切线长定理得到AD=AE=![]() (AB+ACBC),证明△AEF≌△CDE≌△BFD,根据正切的概念计算.
(AB+ACBC),证明△AEF≌△CDE≌△BFD,根据正切的概念计算.
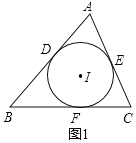
解:如图(1),⊙I是△ABC的内切圆,由切线长定理可得:AD=AE,BD=BF,CE=CF,
AD=AE=![]() [(AB+AC)﹣(BD+CE)]
[(AB+AC)﹣(BD+CE)]
=![]() [(AB+AC)﹣(BF+CF)]
[(AB+AC)﹣(BF+CF)]
=![]() (AB+AC﹣BC),
(AB+AC﹣BC),
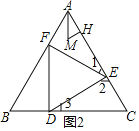
在图(2)中,由于△ABC,△DEF都为正三角形,
∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
∴△AEF≌△CDE(AAS),
同理可证:△AEF≌△CDE≌△BFD,
∴BF=AE,即AF+AE=AF+BF=a.
设M是△AEF的内心,MH⊥AC于H,
则AH=![]() (AE+AF﹣EF)=
(AE+AF﹣EF)=![]() (a﹣b),
(a﹣b),
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AHtan30°=![]() (a﹣b)
(a﹣b)![]() =
=![]() (a﹣b),
(a﹣b),
故答案为:![]() (a﹣b).
(a﹣b).

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目