题目内容
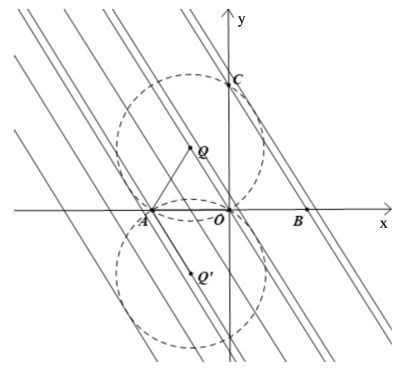
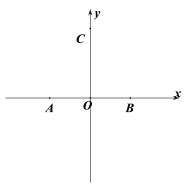
【题目】如图,在平面直角坐标系中,点A与点B关于原点O对称,点A![]() ,点C
,点C![]() ,点P在直线BC上运动.
,点P在直线BC上运动.
(1)连接AC、BC,求证:△ABC是等边三角形;
(2)求点P的坐标,使∠APO=![]() ;
;
(3)在平面内,平移直线BC,试探索:当BC在不同位置时,使∠APO=![]() 的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.
的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.
【答案】(1)见解析;(2)(0,![]() ),(1,
),(1,![]() );(3)见解析.
);(3)见解析.
【解析】
(1)如图(见解析),根据A、B、C三点的坐标求出AB、AC、BC的长,即可得证;
(2)由题(1)的结论可知,![]() ,因此当点P与点C重合,符合条件;如图(见解析),取BC的中点
,因此当点P与点C重合,符合条件;如图(见解析),取BC的中点![]() ,连接
,连接![]() ,由等边三角形性质可得
,由等边三角形性质可得![]() ,则
,则![]() ,故点
,故点![]() 也符合条件,最后根据
也符合条件,最后根据![]() 为BC边上的中点即可求得其坐标;
为BC边上的中点即可求得其坐标;
(3)因为以AO为弦画圆,AO所对的圆心角等于![]() ,则根据圆周角定理得,直线BC与圆的交点P即为满足条件的点,又因这样的圆共有2个:如图(见解析),逐一分析直线BC与两圆的位置关系即可得.
,则根据圆周角定理得,直线BC与圆的交点P即为满足条件的点,又因这样的圆共有2个:如图(见解析),逐一分析直线BC与两圆的位置关系即可得.
(1)根据A、B、C三点的坐标可得:![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
则![]()
故![]() 是等边三角形;
是等边三角形;
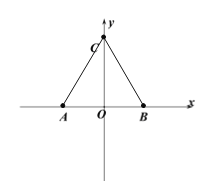
(2)![]() 是等边三角形
是等边三角形
![]()
则当点P与点C重合,符合条件,此时P的坐标为![]() ;
;
当点P与点C不重合时,取BC的中点![]() ,连接
,连接![]()
由等边三角形的性质得:![]()
![]() ,故点
,故点![]() 就是符合条件的点
就是符合条件的点
又![]()
![]() 是等边三角形
是等边三角形
过![]() 作
作![]()
![]()
![]() (
(![]() 是
是![]() 的中位线)
的中位线)
则点![]() 的坐标是
的坐标是![]()
综上,所求点P的坐标为![]() ,
,![]() ;
;
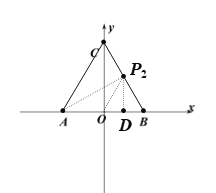
(3)当BC在不同位置时,点P的个数会发生改变,使得![]() 的点P的个数情况共有4种:1个,2个,3个,4个,理由如下:
的点P的个数情况共有4种:1个,2个,3个,4个,理由如下:
如图,以AO为弦画圆,AO所对的圆心角等于![]() 的圆共有2个,记作圆Q和圆
的圆共有2个,记作圆Q和圆![]() ,显然点Q和点
,显然点Q和点![]() 关于x轴对称
关于x轴对称
因为直线BC与圆Q和圆![]() 的公共点P都满足
的公共点P都满足![]()
所以点P的个数情况如下:
①有1个:直线BC与圆Q(或圆![]() )相切
)相切
②有2个:直线BC与圆Q(或圆![]() )相交
)相交
③有3个:直线BC与圆Q(或圆![]() )相切,同时与圆
)相切,同时与圆![]() (或圆Q)相交;直线BC经过圆Q与圆
(或圆Q)相交;直线BC经过圆Q与圆![]() 的一个交点,同时与两圆相交
的一个交点,同时与两圆相交
④有4个:直线BC与圆Q,圆![]() 都相交,且不经过两圆的交点.
都相交,且不经过两圆的交点.