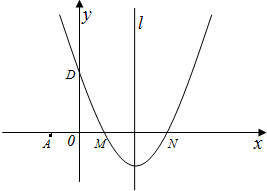题目内容
如图，在平面直角坐标系xOy中，边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上，二次函数y＝－
x2＋bx＋c的图象经过B、C两点．
(1)求该二次函数的解析式；
(2)结合函数的图象探索：当y>0时x的取值范围．
(1)y＝－x2＋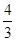
x＋2 (2)－1<x<3
解析解：(1)∵正方形OABC的边长为2
∴B点坐标(2，2)，C点坐标(0，2)．
将B、C两点代入y＝－x2＋bx＋c，得
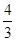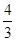解得b＝，∴y＝－x2＋x＋2.
(2)令y＝0，则－x2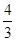＋x＋2＝0，
解得x1＝－1，x2＝3，
∴抛物线与x轴的交点坐标分别为(－1，0)、(3，0)，
结合函数图象，当y>0时，－1<x<3.
练习册系列答案
相关题目
x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．
），点M是抛物线C2：y=mx2-2mx-3m(m<0)的顶点.
.
