题目内容
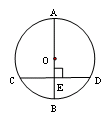
如图,点AB在直线MN上,AB=11㎝,⊙A⊙B的半径均为1㎝,⊙A以每秒2㎝的速度自左向右运动,与此同时,⊙B的半径也不断增长,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0)(10分)

(1)试写出点A,B之间距离d(cm)与时间t(s)之间的函数表达式
(2)问点A出发后多少秒两圆相切?

(1)试写出点A,B之间距离d(cm)与时间t(s)之间的函数表达式
(2)问点A出发后多少秒两圆相切?
t=3, ,11,13
,11,13
 ,11,13
,11,13试题分析:先表示两圆的圆心距,半径差、半径和,再根据两圆内切、外切时,圆心距等于半径差、半径和,列方程求解.
①当2t+t=9时,即t=3秒时,两圆第一次相切;②当2t+t=11时,即t=
 秒时,两圆第二次相切;③当2t-t=11时,即t=11时,两圆第三次相切;④当2t-t=13时,即t=13时,两圆第四次相切.
秒时,两圆第二次相切;③当2t-t=11时,即t=11时,两圆第三次相切;④当2t-t=13时,即t=13时,两圆第四次相切.点评:解答本题的关键是掌握好两圆相切时圆心距与半径之间的关系。

练习册系列答案
相关题目
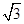 )
)
 △
△ 中,∠
中,∠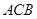 =90o,
=90o,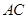 =
=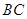 =1,将
=1,将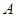 点逆时针旋转30o后得到
点逆时针旋转30o后得到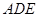 ,点
,点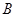 经过的路径为弧
经过的路径为弧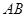 ,则图中阴影部分的面积是 。(结果用
,则图中阴影部分的面积是 。(结果用 表示)
表示)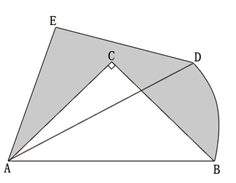
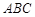 内接于圆
内接于圆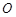 ,动点
,动点 在圆上,且不与B、C重合,则
在圆上,且不与B、C重合,则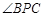 等于( )
等于( )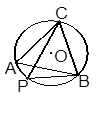
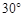 B.
B.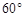 C.60°或120° D. 120°
C.60°或120° D. 120°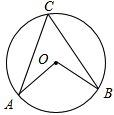


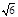 cm
cm  cm
cm 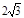 cm
cm 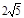 cm
cm