题目内容
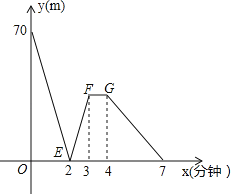
【题目】有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,经过7min同时到达C点,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 .m,甲机器人前2min的速度为 .m/min;
(2)若前3min甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)直接写出两机器人出发多长时间相距28m.
【答案】(1)70, 95;(2)y=35x﹣70;(3)1.2或2.8或4.6min.
【解析】
(1)根据图象结合题意,即可得出A、B两点之间的距离是70m.设甲机器人前2min的速度为xm/min,根据2分钟甲追上乙列出方程,即可求解;
(2)先求出F点的坐标,再设线段EF所在直线的函数解析式为y=kx+b,将E、F(3,35)两点的坐标代入,利用待定系数法即可求解;
(3)设D(0,70),H(7,0),根据图象可知两机器人相距28m时有三个时刻(0~2,2~3,4~7)分别求出DE所在直线的解析式、GH所在直线的解析式,再令y=28,列出方程求解即可.
解:(1)由题意,可得A、B两点之间的距离是70m.
设甲机器人前2min的速度为xm/min,
根据题意,得2(x﹣60)=70,解得x=95.
故答案为70,95;
(2)若前3min甲机器人的速度不变,由(1)可知,前3min甲机器人的速度为95m/min,
则F点纵坐标为:(3﹣2)×(95﹣60)=35,即F(3,35).
设线段EF所在直线的函数解析式为y=kx+b,
将E(2,0),F(3,35)代入,
得![]() ,解得
,解得![]() ,
,
则线段EF所在直线的函数解析式为y=35x﹣70;
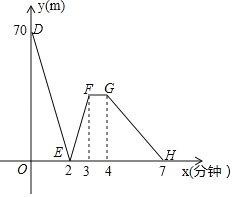
(3)如图,设D(0,70),H(7,0).
∵D(0,70),E(2,0),
∴线段DE所在直线的函数解析式为y=﹣35x+70,
∵G(4,35),H(7,0),
∴线段GH所在直线的函数解析式为![]()
设两机器人出发tmin时相距28m,
由题意,可得﹣35x+70=28,或35x﹣70=28,或![]()
解得t=1.2,或t=2.8,或t=4.6.
即两机器人出发1.2或2.8或4.6min时相距28m.

 阅读快车系列答案
阅读快车系列答案