题目内容
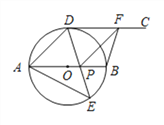
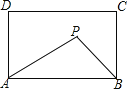
【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
【答案】4![]()
【解析】首先由S△PAB=![]() S矩形ABCD,得出动点P在与AB平行且与AB的距离是2的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.然后在直角三角形ABE中,由勾股定理求得BE的值,即PA+PB的最小值.
S矩形ABCD,得出动点P在与AB平行且与AB的距离是2的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.然后在直角三角形ABE中,由勾股定理求得BE的值,即PA+PB的最小值.
设△ABP中AB边上的高是h.
∵S△PAB=![]() S矩形ABCD,
S矩形ABCD,
∴![]() ABh=
ABh=![]() ABAD,
ABAD,
∴h=![]() AD=2,
AD=2,
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
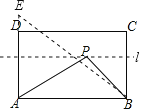
在Rt△ABE中,∵AB=4,AE=2+2=4,
∴BE=![]() ,
,
即PA+PB的最小值为4![]() .
.
故答案为:4![]() .
.

练习册系列答案
相关题目
【题目】某小区2号楼对外销售,已知2号楼某单元共33层,一楼为商铺,只租不售,二楼以上价格如下:第16层售价为6000元/米2,从第16层起每上升一层,每平方米的售价提高30元,反之每下降一层,每平方米的售价降低10元,已知该单元每套的面积均为100米2
(1)请在下表中,补充完整售价y(元/米2)与楼层x(x取正整数)之间的函数关系式.
楼层x(层) | 1楼 | 2≤x≤15 | 16楼 | 17≤x≤33 |
售价y(元/米2) | 不售 |
| 6000 |
|
(2)某客户想购买该单元第26层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算.