题目内容
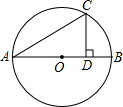
如图，在⊙O中，直径AB与弦CD相交于点P，
=92°，
=46°
（1）求∠BPD的度数；
（2）求证：OC•BP=OP•BD．
 |
| AD |
|
| BC |
（1）求∠BPD的度数；
（2）求证：OC•BP=OP•BD．
（1）∵
=92°，
=46°，
∴∠PBD=46°，∠PDB=23°，
∴∠BPD=180°-46°-23°=111°．
（2）证明：
的度数为46°，
∴∠POC=46°，
在△OPC和△BPD中，∵∠POC=∠PBD=46°，∠OPC=∠BPD，
∴△OPC∽△BPD，
∴
=
，
即OC•BP=OP•BD．
|
| AD |
|
| BC |
∴∠PBD=46°，∠PDB=23°，
∴∠BPD=180°-46°-23°=111°．
（2）证明：
|
| BC |
∴∠POC=46°，
在△OPC和△BPD中，∵∠POC=∠PBD=46°，∠OPC=∠BPD，
∴△OPC∽△BPD，
∴
| OC |
| OP |
| BD |
| BP |
即OC•BP=OP•BD．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
明理由；
