Question

【题目】“十字相乘法”能把二次三项式分解因式，对于形如ax2+bxy+cy2的x，y二次三项式来说，方法的关键是把x2项系数a分解成两个因数a1，a2的积，即a＝a1a2，把y2项系数c分解成两个因数，c1，c2的积，即c＝c1c2，并使a1c2+a2c1正好等于xy项的系数b，那么可以直接写成结果：ax2+bxy+cy2＝（a1x+c1y）（a2x+c2y）

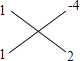
例：分解因式：x2﹣2xy﹣8y2

解：如右图，其中1＝1×1，﹣8＝（﹣4）×2，而﹣2＝1×（﹣4）+1×2∴x2﹣2xy﹣8y2＝（x﹣4y）（x+2y），而对于形如ax2+bxy+cy2+dx+ey+f的x，y的二元二次式也可以用十字相乘法来分解，

如图1，将a分解成mn乘积作为一列，c分解成pq乘积作为第二列，f分解成jk乘积作为第三列，如果mq+np＝b，pk+qj＝e，mk+nj＝d，即第1，2列、第2，3列和第1，3列都满足十字相乘规则，则原式＝（mx+py+j）（nx+qy+k）；

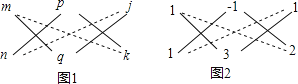
例：分解因式：x2+2xy﹣3y2+3x+y+2

解：如图2，其中1＝1×1，﹣3＝（﹣1）×3，2＝1×2；

而2＝1×3+1×（﹣1），1＝（﹣1）×2+3×1，3＝1×2+1×1；∴x2+2xy﹣3y2+3x+y+2＝（x﹣y+1）（x+3y+2）

请同学们通过阅读上述材料，完成下列问题：

（1）分解因式：6x2﹣7xy+2y2＝　 　x2﹣6xy+8y2﹣5x+14y+6＝　 　

（2）若关于x，y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积，求m的值．

（3）已知x，y为整数，且满足x2+3xy+2y2+2x+4y＝﹣1，求x，y．

Answer 1

【答案】（1）（2x﹣1）（3x﹣2）；（x﹣2y﹣2）（x﹣4y﹣3）（2）43或者﹣78（3）当x＝﹣7时，y＝4；当x＝﹣1时，y＝0

【解析】

（1）结合题意画出图形，即可得出结论；

（2）结合题意画出图形，即可得出结论；

（3）将等式左边先用十字相乘法分解因式，再提取公因式，将右边﹣1改写成1×（﹣1）的形式，由x、y均为整数可得出关于x、y的二元一次方程组，解方程组即可得出结论．

解：（1）如图3，

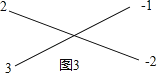
其中6＝2×3，2＝（﹣1）×（﹣2）；而﹣7＝2×（﹣3）+3×（﹣1）；

∴6x2﹣7xy+2y2＝（2x﹣y）（3x﹣2y）．

如图4，

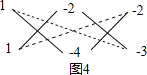
其中1×1＝1，（﹣2）×（﹣4）＝8，（﹣2）×（﹣3）＝6；

而﹣6＝1×（﹣4）+1×（﹣2），﹣5＝1×（﹣3）+1×（﹣2），14＝（﹣2）×（﹣3）+（﹣4）×（﹣2）；

∴x2﹣6xy+8y2﹣5x+14y+6＝（x﹣2y﹣2）（x﹣4y﹣3）．

故答案为：（2x﹣1）（3x﹣2）；（x﹣2y﹣2）（x﹣4y﹣3）．

（2）如图5，

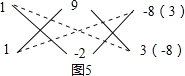
∵关于x，y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积，

∴存在：其中1×1＝1，9×（﹣2）＝﹣18，（﹣8）×3＝﹣24；

而7＝1×（﹣2）+1×9，﹣5＝1×（﹣8）+1×3，m＝9×3+（﹣2）×（﹣8）＝43或m＝9×（﹣8）+（﹣2）×3＝﹣78．

故若关于x，y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积，m的值为43或者﹣78．

（3）∵x2+3xy+2y2+2x+4y＝（x+2y）（x+y）+2（x+2y）＝（x+2y）（x+y+2）＝﹣1＝1×（﹣1），且x、y为整数，

∴有，或，

解得：或．

故当x＝﹣7时，y＝4；当x＝﹣1时，y＝0．