题目内容
如图,在等腰直角三角形ABC中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连结PC,若△ABC的面积为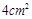 ,则△BPC的面积为( )
,则△BPC的面积为( )
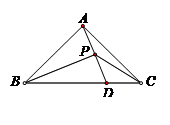
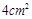 ,则△BPC的面积为( )
,则△BPC的面积为( )
A.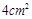 | B. | C.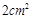 | D.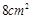 |
C.
试题分析:根据等腰三角形三线合一的性质可得AP=PD,然后根据等底等高的三角形面积相等求出△BPC的面积等于△ABC面积的一半,代入数据计算即可得解.
∵BD=BA,BP是∠ABC的平分线,
∴AP=PD,
∴S△BPD=
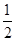 S△ABD,S△CPD=
S△ABD,S△CPD=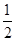 S△ACD,
S△ACD,∴S△BPC=S△BPD+S△CPD=
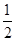 S△ABD+S△ACD=S△ABC,
S△ABD+S△ACD=S△ABC,∵△ABC的面积为4cm2,
∴S△BPC=
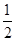 ×4=2cm2.
×4=2cm2.故选C.
考点: 1.等腰直角三角形;2.三角形的面积;3.等腰三角形的性质.

练习册系列答案
相关题目
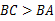 ,
,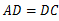 ,BD平分∠ABC.
,BD平分∠ABC.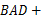 ∠
∠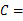 180°.
180°.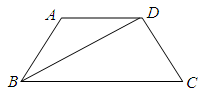
 ,OB与x轴所夹锐角是45°
,OB与x轴所夹锐角是45°
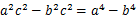 ,-------------------①
,-------------------① .----------②
.----------②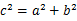 .---------------------------------------③
.---------------------------------------③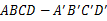 中,
中,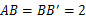 ,
,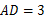 ,一只蚂蚁从
,一只蚂蚁从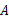 点出发,沿长方体表面爬到
点出发,沿长方体表面爬到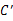 点,求蚂蚁怎样走最短,最短路程是多少?
点,求蚂蚁怎样走最短,最短路程是多少?
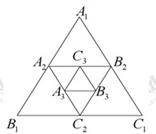
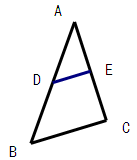
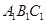 的面积为1,取△
的面积为1,取△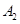 、
、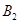 、
、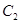 ,作第二个正三角形△
,作第二个正三角形△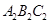 ,再取△
,再取△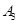 、
、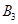 、
、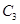 ,作第三个正三角形△
,作第三个正三角形△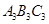 ,…用同样的方法作正三角形,则第2个正三角形△
,…用同样的方法作正三角形,则第2个正三角形△ 的面积是 .
的面积是 .