题目内容
【题目】已知二次函数 y＝mx2﹣2mx+n 的图象经过（0，﹣3）．
（1）n＝ _____________；
（2） 若二次函数 y＝mx2﹣2mx+n 的图象与 x 轴有且只有一个交点，求 m 值；
（3） 若二次函数 y＝mx2﹣2mx+n 的图象与平行于 x 轴的直线 y＝5 的一个交点的横坐标为4，则另一个交点的坐标为 ；
（4） 如图，二次函数 y＝mx2﹣2mx+n 的图象经过点 A（3，0），连接 AC，点 P 是抛物线位于线段 AC 下方图象上的任意一点，求△PAC 面积的最大值．
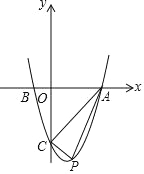
【答案】（1）－3；（2）m=﹣3；（3）（﹣2，5）；（4）当a=
时，△PAC的面积取最大值，最大值为
【解析】
（1）将（0，-3）代入二次函数解析式中即可求出n值；
（2）由二次函数图象与x轴只有一个交点，利用根的判别式△=0，即可得出关于m的一元二次方程，解之取其非零值即可得出结论；
（3）根据二次函数的解析式利用二次函数的性质可找出二次函数图象的对称轴，利用二次函数图象的对称性即可找出另一个交点的坐标；
（4）将点A的坐标代入二次函数解析式中可求出m值，由此可得出二次函数解析式，由点A、C的坐标，利用待定系数法可求出直线AC的解析式，过点P作PD⊥x轴于点D，交AC于点Q，设点P的坐标为（a，a2-2a-3），则点Q的坐标为（a，a-3），点D的坐标为（a，0），根据三角形的面积公式可找出S△ACP关于a的函数关系式，配方后即可得出△PAC面积的最大值．
解:（1）∵二次函数y=mx2﹣2mx+n的图象经过（0，﹣3），
∴n=﹣3．
故答案为：﹣3．
（2）∵二次函数y=mx2﹣2mx﹣3的图象与x轴有且只有一个交点，
∴△=（﹣2m）2﹣4×（﹣3）m=4m2+12m=0，
解得：m1=0，m2=﹣3．
∵m≠0，
∴m=﹣3．
（3）∵二次函数解析式为y=mx2﹣2mx﹣3，
∴二次函数图象的对称轴为直线x=﹣
=1．
∵该二次函数图象与平行于x轴的直线y=5的一个交点的横坐标为4，
∴另一交点的横坐标为1×2﹣4=﹣2，
∴另一个交点的坐标为（﹣2，5）．
故答案为：（﹣2，5）．
（4）∵二次函数y=mx2﹣2mx﹣3的图象经过点A（3，0），
∴0=9m﹣6m﹣3，
∴m=1，
∴二次函数解析式为y=x2﹣2x﹣3．
设直线AC的解析式为y=kx+b（k≠0），
将A（3，0）、C（0，﹣3）代入y=kx+b，得：
，解得：
，
∴直线AC的解析式为y=x﹣3．
过点P作PD⊥x轴于点D，交AC于点Q，如图所示．
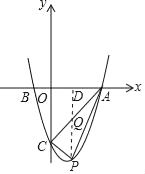
设点P的坐标为（a，a2﹣2a﹣3），则点Q的坐标为（a，a﹣3），点D的坐标为（a，0），
∴PQ=a﹣3﹣（a2﹣2a﹣3）=3a﹣a2，
∴S△ACP=S△APQ+S△CPQ=
PQOD+PQAD=﹣a2+
a=﹣（a﹣）2+，
∴当a=时，△PAC的面积取最大值，最大值为 ．
