题目内容
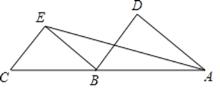
【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=![]() AB.
AB.
(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

【答案】(1)6,(6,3);(2)①![]() ;②
;②![]() 为
为![]() 或6.
或6.
【解析】
(1)由平移的性质可得四边形ABCD是平行四边形,可得AB=CD=6,由题意可求点C坐标;
(2)由题意列出方程,可求解;
(3)分两种情况讨论,列出方程可求解.
(1)∵点A(-2,0),点B坐标为(4,0),
∴AB=6
∵将AD沿x轴向右平移至BC的位置,
∴AD∥BC,AD=BC
∴四边形ABCD是平行四边形
∴CD=AB=6,CD∥AB
∵OD=![]() AB.
AB.
∴OD=3,且CD∥AB
∴点C(6,3)
故答案为:6,(6,3);
(2)∵MN∥y轴,
∴点N在CD上,
∴4-t=t-3
∴t=![]()
∴当t=![]() s时,MN∥y轴;
s时,MN∥y轴;
(3)当点N在OD上时,
∵S△BCM=2S△ADN.
∴![]() ×3×t=2×
×3×t=2×![]() ×2×(3-t)
×2×(3-t)
解得:t=![]()
当点N在CD上时,
∵S△BCM=2S△ADN.
∴![]() ×3×t=2×
×3×t=2×![]() ×3×(t-3)
×3×(t-3)
解得:t=6
综上所述:t=6或![]() 时,S△BCM=2S△ADN.
时,S△BCM=2S△ADN.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目