题目内容
【题目】三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图，△ABC中，AB=AC，且∠A=36°．
（1）在图中用尺规作边AB的垂直平分线交AC于D，连接BD（保留作图痕迹，不写作法）．
（2）请问△BDC是不是黄金三角形，如果是，请给出证明，如果不是，请说明理由．
【答案】（1）详见解析；（2）△BDC是黄金三角形，详见解析
【解析】
（1）可根据基本作图中线段垂直平分线的作法进行作图；
（2）求得各个角的度数，根据题意进行判断．
解：（1）如图所示
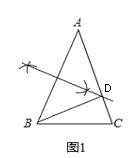
（2）△BDC是黄金三角形
∵ED是AB的垂直平分线
∴ AD=BD
∴∠ABD=∠A=36°
而在等腰△ABC中，∠ABC=∠C=72°
∴∠CBD=∠ABC－∠ABD=72°－36°=36°
∴∠BDC=180°－∠C－∠CBD=180°－72°－36°=72°
∴△BDC是等腰三角形且顶角∠CBD=36°
∴△BDC是黄金三角形．
练习册系列答案
导学全程练创优训练系列答案
相关题目
