题目内容
【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
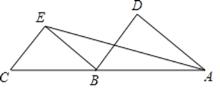
【答案】(1)见解析;(2)60°
【解析】
(1)根据平行线的判定得出BE∥AD,根据平行线的性质得出∠D=∠EBD,求出∠BEC=∠EBD,根据平行线的判定得出即可;
(2)根据平行线的性质得出∠C=∠DBA,∠EBC=∠DAC,即可求出答案.
(1)证明:∵∠DAE=∠AEB,
∴BE∥AD,
∴∠D=∠EBD,
∵∠D=∠BEC,
∴∠BEC=∠EBD,
∴BD∥EC;
(2)解:∵BD∥CE,BE∥AD,
∴∠C=∠DBA,∠EBC=∠DAC,
∵∠C=70°,∠DAC=50°,
∴∠DBA=70°,∠EBC=50°,
∴DBE=180°-∠DBA-∠EBC=60°.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目