题目内容
【题目】已知等边三角形
的高为6，在这个三角形所在的平面内有一个点
，若点到
的距离是1，点到
的距离是2，则点到
的最小距离与最大距离分别是_______.
【答案】3和9
【解析】
根据题意画出相应的图形，直线DM与直线NF都与AB的距离为1，直线NG与直线ME都与AC的距离为2，当P与N重合时，HN为P到BC的最小距离；当P与M重合时，MQ为P到BC的最大距离，根据题意得到△NFG与△MDE都为等边三角形，利用锐角三角函数定义及特殊角的三角函数值求出DB与FB的长，以及CG与CE的长，进而由DB+BC+CE求出DE的长，由BC-BF-CG求出FG的长，求出等边三角形NFG与等边三角形MDE的高，即可确定出点P到BC的最小距离和最大距离．
解：根据题意画出相应的图形，直线DM与直线NF都与AB的距离为1，直线NG与直线ME都与AC的距离为2，
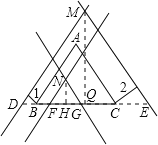
当P与N重合时，HN为P到BC的最小距离；当P与M重合时，MQ为P到BC的最大距离，
根据题意得到△NFG与△MDE都为等边三角形，
∵等边三角形ABC的高为6
∴等边三角形ABC的边长：BC=
∴DB=FB
，CE=CG
，
∴DE=DB+BC+CE=
+
=
，
FG=BC-BF-CG=
∴NH=3，MQ=9
则点P到BC的最小距离和最大距离分别是3，9．
故答案为：3，9．
练习册系列答案
阅读快车系列答案
相关题目
