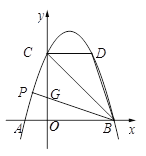题目内容
【题目】如下图①,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(![]() ,0),B(3,0),与y轴交于点C,连接BC.
,0),B(3,0),与y轴交于点C,连接BC.
(1)求抛物线的表达式;
(2)抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请直接写出点M的坐标;若不存在,请说明理由;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.

【答案】(1)、y=-![]() +2x+3;(2)、M1(
+2x+3;(2)、M1(![]() ,
, ![]() ),M2(
),M2(![]() ,
, ![]() );(3)、(
);(3)、(![]() ,
, ![]() )
)
【解析】试题分析:(1)、利用待定系数法求出二次函数的解析式;(2)、根据等面积法得出点M的坐标;(3)、首先根据二次函数的解析式求出点C和点D的坐标,从而得出CD∥x轴,根据题意得出△CGB和△CDB全等,得出点G的坐标,利用待定系数法求出直线BP的函数解析式,然后求出一次函数和二次函数的交点坐标,根据点P在抛物线的左侧得出点P的坐标.
试题解析:(1)、∵抛物线![]() 与x轴交于点A(
与x轴交于点A(![]() ,0),B(3,0),
,0),B(3,0),
![]() ,解得
,解得![]() , ∴抛物线的表达式为
, ∴抛物线的表达式为![]() .
.
(2)、存在.M1(![]() ,
, ![]() ),M2(
),M2(![]() ,
, ![]() )
)
(3)、存在.如图,设BP交轴y于点G. ∵点D(2,m)在第一象限的抛物线上,
∴当x=2时,m=![]() . ∴点D的坐标为(2,3).
. ∴点D的坐标为(2,3).
把x=0代入![]() ,得y=3. ∴点C的坐标为(0,3). ∴CD∥x轴,CD = 2.
,得y=3. ∴点C的坐标为(0,3). ∴CD∥x轴,CD = 2.
∵点B(3,0),∴OB =" OC" = 3 ∴∠OBC=∠OCB=45°.
∴∠DCB=∠OBC=∠OCB=45°,又∵∠PBC=∠DBC,BC=BC,
∴△CGB ≌ △CDB(ASA),∴CG=CD=2. ∴OG=OC![]() CG=1,∴点G的坐标为(0,1).
CG=1,∴点G的坐标为(0,1).
设直线BP的解析式为y=kx+1,将B(3,0)代入,得3k+1=0,解得k=![]() .
.
∴直线BP的解析式为y=![]() x+1. 令
x+1. 令![]() x+1=
x+1=![]() .解得
.解得![]() ,
, ![]() .
.
∵点P是抛物线对称轴x=![]() =1左侧的一点,即x<1,∴x=
=1左侧的一点,即x<1,∴x=![]() .把x=
.把x=![]() 代入抛物线
代入抛物线![]() 中,解得y=
中,解得y=![]() ∴当点P的坐标为(
∴当点P的坐标为(![]() ,
, ![]() )时,满足∠PBC=∠DBC.
)时,满足∠PBC=∠DBC.