题目内容
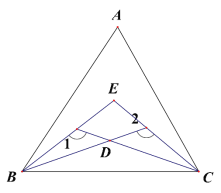
【题目】(1)如图,△ABC, ∠ABC、∠ACB 的三等分线交于点 E、D, 若∠1=130°,∠2=110°,求∠A 的度数。
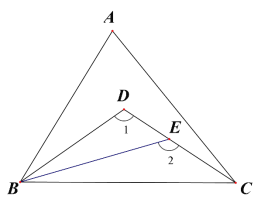
(2)如图,△ABC,∠ABC 的三等分线分别与∠ACB 的平分线交于点 D,E 若∠1=110°,∠2=130°,求∠A 的度数。
【答案】(1)∠A=60°,(2)∠A=60°
【解析】
(1)由三角形内角和及三等角平分线的定义可得到方程组,则可求得∠ABC+∠ACB,再利用三角形内角和可求得∠A.
(2)由三角形外角可得∠DBC=20°由三等角平分线的定义可得∠ABC=60°,三角形内角和可得∠ECB=30°,角平分线的定义可得∠ACB=60°,由三角形内角和可得∠A=60°。
解:(1)
∵∠ABC、∠ACB 的三等分线交于点 E、D
![]()
![]() , ∠ABC=3x,∠ACB=3y
, ∠ABC=3x,∠ACB=3y
![]()

①+②得:240°+3x+3y=360°
即3x+3y=120°
∴∠ABC+∠ACB=120°
∴∠A=180°-(∠ABC+∠ACB)=180°-120°=60°
(2)∵∠ABC 的三等分线分别与∠ACB 的平分线交于点 D,E
![]()
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






