题目内容
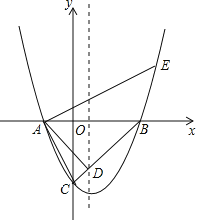
【题目】如图所示,已知在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (其中
(其中![]() 、
、![]() 为常数,且
为常数,且![]() )与
)与![]() 轴交于点
轴交于点![]() ,它的坐标是
,它的坐标是![]() ,与
,与![]() 轴交于点
轴交于点![]() ,此抛物线顶点
,此抛物线顶点![]() 到
到![]() 轴的距离为4.
轴的距离为4.
(1)求抛物线的表达式;
(2)求![]() 的正切值;
的正切值;
(3)如果点![]() 是抛物线上的一点,且
是抛物线上的一点,且![]() ,试直接写出点
,试直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 或
或![]()
【解析】
(1)先求得抛物线的对称轴方程,然后再求得点C的坐标,设抛物线的解析式为y=a(x+1)2+4,将点(-3,0)代入求得a的值即可;
(2)先求得A、B、C的坐标,然后依据两点间的距离公式可得到BC、AB、AC的长,然后依据勾股定理的逆定理可证明∠ABC=90°,最后,依据锐角三角函数的定义求解即可;
(3)记抛物线与x轴的另一个交点为D.先求得D(1,0),然后再证明∠DBO=∠CAB,从而可证明∠CAO=ABD,故此当点P与点D重合时,∠ABP=∠CAO;当点P在AB的上时.过点P作PE∥AO,过点B作BF∥AO,则PE∥BF.先证明∠EPB=∠CAB,则tan∠EPB=![]() ,设BE=t,则PE=3t,P(-3t,3+t),将P(-3t,3+t)代入抛物线的解析式可求得t的值,从而可得到点P的坐标.
,设BE=t,则PE=3t,P(-3t,3+t),将P(-3t,3+t)代入抛物线的解析式可求得t的值,从而可得到点P的坐标.
解:(1)抛物线的对称轴为x=-![]() =-1.
=-1.
∵a<0,
∴抛物线开口向下.
又∵抛物线与x轴有交点,
∴C在x轴的上方,
∴抛物线的顶点坐标为(-1,4).
设抛物线的解析式为y=a(x+1)2+4,将点(-3,0)代入得:4a+4=0,解得:a=-1,
∴抛物线的解析式为y=-x2-2x+3.
(2)将x=0代入抛物线的解析式得:y=3,
∴B(0,3).
∵C(-1,4)、B(0,3)、A(-3,0),
∴BC=![]() ,AB=3
,AB=3![]() ,AC=2
,AC=2![]() ,
,
∴BC2+AB2=AC2,
∴∠ABC=90°.
∴![]() .
.
即![]() 的正切值等于
的正切值等于![]() .
.
(3)如图1所示:记抛物线与x轴的另一个交点为D.
∵点D与点A关于x=-1对称,
∴D(1,0).
∴tan∠DBO=![]() .
.
又∵由(2)可知:tan∠CAB=![]() .
.
∴∠DBO=∠CAB.
又∵OB=OA=3,
∴∠BAO=∠ABO.
∴∠CAO=∠ABD.
∴当点P与点D重合时,∠ABP=∠CAO,
∴P(1,0).
如图2所示:当点P在AB的上时.过点P作PE∥AO,过点B作BF∥AO,则PE∥BF.
∵BF∥AO,
∴∠BAO=∠FBA.
又∵∠CAO=∠ABP,
∴∠PBF=∠CAB.
又∵PE∥BF,
∴∠EPB=∠PBF,
∴∠EPB=∠CAB.
∴tan∠EPB=![]() .
.
设BE=t,则PE=3t,P(-3t,3+t).
将P(-3t,3+t)代入抛物线的解析式得:y=-x2-2x+3得:-9t2+6t+3=3+t,解得t=0(舍去)或t=![]() .
.
∴P(-![]() ,
,![]() ).
).
综上所述,点P的坐标为P(1,0)或P(-![]() ,
,![]() ).
).

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案