题目内容
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
【答案】(1)y=﹣x2+2x+8,其顶点为(1,9)(2)y=﹣x2+2x+3
【解析】试题分析:(1)根据对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0),可得 ,解得
,解得![]() 即可求解,(2)设令平移后抛物线为
即可求解,(2)设令平移后抛物线为![]() ,
,
可得D(1,k),B(0,k-1),且![]() ,根据BC平行于x轴,可得点C与点B关于对称轴x=1对称,可得C(2,k-1), 根据
,根据BC平行于x轴,可得点C与点B关于对称轴x=1对称,可得C(2,k-1), 根据![]() ,解得
,解得![]() ,即
,即![]() .
.
作DH⊥BC于H,CT⊥x轴于T, 则在△DBH中,HB=HD=1,∠DHB=90°,
又AC∥BD,得△CTA∽△DHB,所以CT=AT,即![]() ,
,
解得k=4,即可求平移后的二次函数解析式.
试题解析:(1)由题意得: 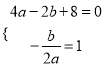 ,解得:
,解得: ![]() ,
,
所以抛物线的表达式为![]() ,其顶点为(1,9).
,其顶点为(1,9).
(2)令平移后抛物线为![]() ,
,
易得D(1,k),B(0,k-1),且![]() ,
,
由BC平行于x轴,知点C与点B关于对称轴x=1对称,得C(2,k-1),
由![]() ,解得
,解得![]() (舍正),即
(舍正),即![]() .
.
作DH⊥BC于H,CT⊥x轴于T,
则在△DBH中,HB=HD=1,∠DHB=90°,
又AC∥BD,得△CTA∽△DHB,
所以CT=AT,即![]() ,
,
解得k=4,
所以平移后抛物线表达式为![]() .
.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某山区有若干名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,资助一名小学生的学习费用需要b元.某校学生积极捐款,初中各年级学生捐款数额与其捐助贫困中学生和小学生人数的部分情况如下表:
捐款数额/元 | 资助贫困中学生人数/名 | 资助贫困小学生人数/名 | |
七年级 | 4000 | 2 | 4 |
八年级 | 4200 | 3 | 3 |
九年级 | 5000 |
(1)求a,b的值;
(2)九年级学生的捐款恰好解决了剩余贫困中小学生的学习费用,请计算九年级学生可捐助的贫困小学生人数.