题目内容
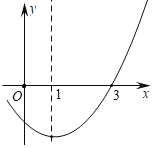
【题目】如图抛物线y=ax2+bx+c的对称轴是x=﹣1,与x轴的一个交点为(﹣5,0),则不等式ax2+bx+c>0的解集为_____.
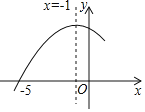
【答案】﹣5<x<3
【解析】
先根据抛物线的对称性得到A点坐标(3,0),由y=ax2+bx+c>0得函数值为正数,即抛物线在x轴上方,然后找出对应的自变量的取值范围即可得到不等式ax2+bx+c>0的解集.
解:根据图示知,抛物线y=ax2+bx+c图象的对称轴是x=﹣1,与x轴的一个交点坐标为(﹣5,0),
根据抛物线的对称性知,抛物线y=ax2+bx+c图象与x轴的两个交点关于直线x=﹣1对称,即
抛物线y=ax2+bx+c图象与x轴的另一个交点与(﹣5,0)关于直线x=﹣1对称,
∴另一个交点的坐标为(3,0),
∵不等式ax2+bx+c>0,即y=ax2+bx+c>0,
∴抛物线y=ax2+bx+c的图形在x轴上方,
∴不等式ax2+bx+c>0的解集是﹣5<x<3.
故答案为﹣5<x<3.

练习册系列答案
相关题目