Question

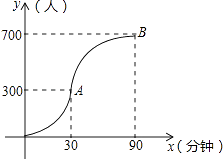
【题目】如图，在直角坐标系中有一直角三角形AOB，O为坐标原点，OA=1，tan∠BAO=3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y=ax2+bx+c经过点A，B，C．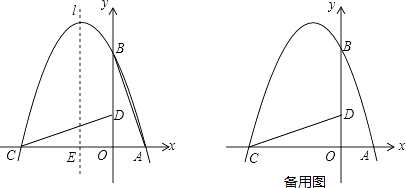

（1）求抛物线的解析式；
（2）若点P是第二象限内抛物线上的动点，其横坐标为t，
①设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求出当△CEF与△COD相似时，点P的坐标；
②是否存在一点P，使△PCD的面积最大？若存在，求出△PCD的面积的最大值；若不存在，请说明理由．

Answer 1

【答案】
（1）解：在Rt△AOB中，OA=1，tan∠BAO= =3，

∴OB=3OA=3．

∵△DOC是由△AOB绕点O逆时针旋转90°而得到的，

∴△DOC≌△AOB，

∴OC=OB=3，OD=OA=1，

∴A、B、C的坐标分别为（1，0），（0，3）（﹣3，0）．

代入解析式为

，

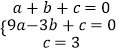解得： ．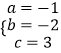

∴抛物线的解析式为y=﹣x2﹣2x+3

（2）解：①∵抛物线的解析式为y=﹣x2﹣2x+3，

∴对称轴l=﹣ =﹣1，

∴E点的坐标为（﹣1，0）．

如图，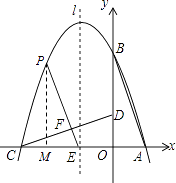

当∠CEF=90°时，△CEF∽△COD．此时点P在对称轴上，即点P为抛物线的顶点，P（﹣1，4）；

当∠CFE=90°时，△CFE∽△COD，过点P作PM⊥x轴于点M，则△EFC∽△EMP．

∴ ，

∴MP=3EM．

∵P的横坐标为t，

∴P（t，﹣t2﹣2t+3）．

∵P在第二象限，

∴PM=﹣t2﹣2t+3，EM=﹣1﹣t，

∴﹣t2﹣2t+3=﹣（t﹣1）（t+3），

解得：t1=﹣2，t2=﹣3（因为P与C重合，所以舍去），

∴t=﹣2时，y=﹣（﹣2）2﹣2×（﹣2）+3=3．

∴P（﹣2，3）．

∴当△CEF与△COD相似时，P点的坐标为：（﹣1，4）或（﹣2，3）；

②设直线CD的解析式为y=kx+b，由题意，得

，

解得： ，

∴直线CD的解析式为：y= x+1．

设PM与CD的交点为N，则点N的坐标为（t， t+1），

∴NM= t+1．

∴PN=PM﹣NM=﹣t2﹣2t+3﹣（ t+1）=﹣t2﹣ +2．

∵S△PCD=S△PCN+S△PDN，

∴S△PCD= PNCM+ PNOM

= PN（CM+OM）

= PNOC

= ×3（﹣t2﹣ +2）

=﹣ （t+ ）2+ ，

∴当t=﹣ 时，S△PCD的最大值为 ．

【解析】（1）先求出A、B、C的坐标，再用待定系数法就可以直接求出二次函数的解析式；（2）①抛物线的解析式为y=﹣x2﹣2x+3，故可以求出抛物线的对称轴，分类讨论当∠CEF=90°时，△CEF∽△COD．此时点P在对称轴上，即点P为抛物线的顶点，当∠CFE=90°时，△CFE∽△COD，过点P作PM⊥x轴于点M，则△EFC∽△EMP．根据相似三角形的性质即可求出P点的坐标；②设直线CD的解析式为y=kx+b，由待定系数法即可求出解析式，设PM与CD的交点为N，根据CD的解析式表示出点N的坐标，再根据S△PCD=S△PCN+S△PDN，就可以表示出△PCD的面积，利用顶点式就可以求出结论。
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a才能正确解答此题．