题目内容
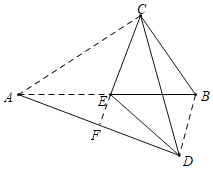
【题目】如图△ABC中,∠ACB=90°,AC=8,BC=6,点E是AB中点,将△CAE沿着直线CE翻折,得到△CDE,连接AD,则点E到线段AD的距离等于( )

A.2B.1.8C.1.5D.1.4
【答案】D
【解析】
延长CE交AD于F,连接BD,先判定△ABC∽△CAF,即可得到CF=6.4,从而求得EF=CF-CE=1.4.
解:如图,延长CE交AD于F,连接BD,由折叠性质可知,EF⊥AD,
∵∠ACB=90°,AC=8,BC=6,
∴AB=10,
∵∠ACB=90°,CE为中线,
∴CE=AE=BE,
∴∠ACF=∠BAC,
又∵∠AFC=∠BCA=90°,
∴△ABC∽△CAF,
∴![]() ,即
,即![]() ,
,
∴CF=6.4,
∴EF=CF-CE=1.4,
故选:D.

练习册系列答案
相关题目