题目内容
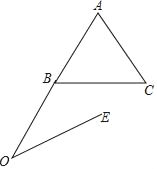
【题目】如图,等边△ABC中,AB=3,点O在AB的延长线上,OA=6,且∠AOE=30°,动点P从点O出发,以每秒![]() 个单位的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从点B出发,以每秒1个单位的速度沿折线B…C…A向点A运动,Q与A重合时,P、Q同时停止运动,设P的运动时间为t秒.
个单位的速度沿射线OE方向运动,以P为圆心,OP为半径作⊙P,同时点Q从点B出发,以每秒1个单位的速度沿折线B…C…A向点A运动,Q与A重合时,P、Q同时停止运动,设P的运动时间为t秒.
(1)当△POB是直角三角形时,求t的值;
(2)当⊙P过点C时,求⊙P与线段OA围成的封闭图形的面积;
(3)当⊙P与△ABC的边所在直线相切时,求t的值;
(4)当线段OQ与⊙P只有一个公共点时,直接写出t的取值范围.
【答案】(1)t=![]() 或t=2时△POB是直角三角形;(2)
或t=2时△POB是直角三角形;(2)![]() 或
或![]() ;(3)当t=1或t=
;(3)当t=1或t=![]() 时⊙P与△ABC的边所在直线相切;(4)
时⊙P与△ABC的边所在直线相切;(4)![]() <t≤6时,线段OQ与⊙P只有一个公共点.
<t≤6时,线段OQ与⊙P只有一个公共点.
【解析】
(1)首先证明O、C、E共线,分两种情形分别讨论求解即可解决问题;
(2)分两种情形求解即可.
(3))⊙P不可能与AB所在直线相切当⊙P与AC所在直线相切时,如图4中,求出OP的长即可解决问题,当⊙P与BC的边所在直线相切时,如图5中,求出OP即可;
(4)如图6中,当⊙P经过点Q时,求出t的值,即可解决问题;
(1)如图1中,连接OC.
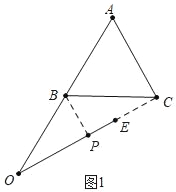
∵∠ABC=60°,OB=BC
∴∠AOC=∠BCO=30°,
∴OE经过点C,∠ACO=90°
如图当∠BPO=90°时,OP=OBcos30=![]() ,
,
∴t=![]() .
.
如图2中,当∠PBO=90°时,
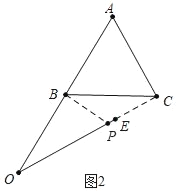
OP=![]() =2
=2![]() ,
,
∴t=2,
∴当t=![]() 或t=2时△POB是直角三角形.
或t=2时△POB是直角三角形.
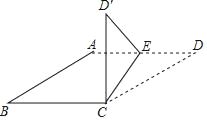
(2)如图3中,当点P运动到OC中点时⊙P过点C,设⊙P交OA于点F,作PH⊥OA于H.
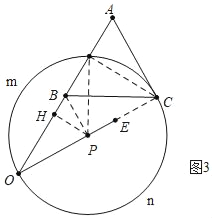
∵PO=PF
∴∠O=∠PFO=30°,
∴∠OPF=120°
又∵PO═![]() ,
,
∴PH=![]() OP=
OP=![]() ,
,
∴S弓形OmF=S扇形POF﹣S△OPF=![]() π﹣
π﹣![]() 或S弓形OnF=
或S弓形OnF=![]() π+
π+![]() .
.
(3)⊙P不可能与AB所在直线相切
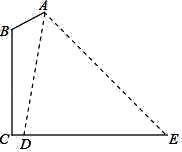
当⊙P与AC所在直线相切时,如图4中,
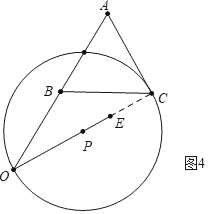
∵∠ACO=90°
∴当点P运动到OC中点时⊙P与AC边所在直线相切,此时t=![]()
当⊙P与BC的边所在直线相切时,如图5中,此时PB=OP=![]() ,t=1,
,t=1,
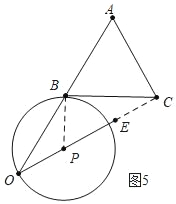
∴当t=1或t=![]() 时⊙P与△ABC的边所在直线相切.
时⊙P与△ABC的边所在直线相切.
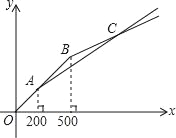
(4)如图6中,当⊙P经过点Q时,
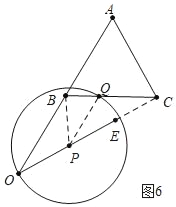
∵BC:BQ=CO:OP=![]() ,
,
∴PQ∥OB,
∴![]() ,
,
∴![]() ,
,
解得t=![]() ,
,
观察图象可知:当![]() <t≤6时,线段OQ与⊙P只有一个公共点.
<t≤6时,线段OQ与⊙P只有一个公共点.