Question

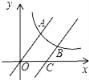
【题目】如图，直线与双曲线交于点A．将直线向右平移6个单位后，与双曲线交于点B，与x轴交于点C，若，则k的值为（　　）

A. 12 B. 14 C. 18 D. 24

Answer 1

【答案】A

【解析】

试题作AD⊥x轴于D点，BE⊥x轴于E，根据平移得到C点坐标为（6，0），再证明Rt△AOD∽Rt△BCE，利用相似比得到OD=2CE，AD=2BE，设CE=t，则OD=2t，OE=6+t，然后表示A点坐标（2t，），B点坐标（6+t，），再根据反比例函数图象上点的坐标特征得到2t=（6+t），解得t1=0（舍去），t2=2，于是A点坐标为（4，3），最后把A点坐标代入y=即可确定k的值．

试题解析：作AD⊥x轴于D点，BE⊥x轴于E，如图，

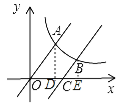
∵直线y=向右平移6个单位得到直线OC，

∴C点坐标为（6，0），

∵OA∥BC，

∴∠AOD=∠BCE，

∴Rt△AOD∽Rt△BCE，

∴，

∴OD=2CE，AD=2BE，

设CE=t，则OD=2t，OE=6+t，

当x=2t时，y=，即A点坐标为（2t，）

∴BE=，

∴B点坐标为（6+t，），

∴2t=（6+t），

解得t1=0（舍去），t2=2，

∴A点坐标为（4，3），

把A点坐标为（4，3）代入y=得k=3×4=12．

故选A．