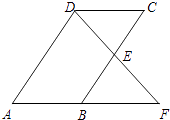
��Ŀ����
����Ŀ��ijѧУ��չ��������Ƽ����±������,��ϲ�����������������һ��ң�س���ֱ�߹��AC������ֱ���˶���ģ��.�ס�������ͬʱ�ֱ��A,B����,�ع������C��,��AC��,���ٶ����ҵ��ٶȵ�1.5��,��t�ֺ�ס�����ң�س���B���ľ���ֱ�Ϊd1,d2(��λ:��),��d1,d2��t�ĺ�����ϵ��ͼ,�Ը���ͼ������������.

��1��������ҵ��ٶ�v2=________��/��;
��2��д��d1��t�ĺ�������ʽ;
��3�����ס�����ң�س��ľ��볬��10��ʱ�źŲ�����������,��̽��ʲôʱ����ң�س����źŲ�����������?
���𰸡���1��40����2����0��t��1ʱ��d1=��60t+60����1��t��3ʱ��d1=60t��60����3����0��t��2��5ʱ����ң�س����źŲ����������ţ�
��������
���⣨1������·����ʱ��Ĺ�ϵ���ɵô𰸣�
��2�����ݼ��ٶ����ҵ��ٶȵ�1��5�����ɵü��ٶȣ�����·����ʱ��Ĺ�ϵ���ɵ�a��ֵ�����ݴ���ϵ�������ɵô𰸣�
��3�����������ľ��룬�ɵò���ʽ�����ݽⲻ��ʽ���ɵô𰸣�
�����������1���ҵ��ٶ�v2=120��3=40����/�֣���
��2��v1=1��5v2=1��5��40=60����/�֣���
60��60=1�����ӣ���a=1��
d1=![]() ��
��
��3��d2=40t��
��0��t��1ʱ��d2-d1��10��
��-60t+60+40t��10��
���0��t��2��5��
��0��t��1��
����0��t��1ʱ����ң�س����źŲ����������ţ�
��1��t��3ʱ��d2-d1��10��
��40t-��60t-60����10��
��1��t��![]() ʱ����ң�س����źŲ�����������
ʱ����ң�س����źŲ�����������
������������0��t��2��5ʱ����ң�س����źŲ����������ţ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ijУ�ڡ�626���ʽ����ա�ǰ��֯���꼶ȫ��ѧ��320�˽�����һ�Ρ���ƷԤ��֪ʶ�����������������ȡ�˲���ѧ���ɼ�����ͳ�ƣ��������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ���ṩ����Ϣ������������⣺
�ٷ����Σ�x��ʾ������ | Ƶ�� | Ƶ�� |
50��x��60 | 4 | 0.1 |
60��x��70 | a | 0.2 |
70��x��80 | 12 | b |
80��x��90 | 10 | 0.25 |
90��x��100 | 6 | 0.15 |

��1������a= �� b= �� ����ȫֱ��ͼ
��2����������ͳ��ͼ�����˳ɼ��ֲ�������������80��x��100��Ӧ���ε�Բ�ĽǶ�������
��3������Ƹ��꼶������60��x��100��ѧ���ж����ˣ�