题目内容
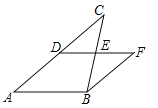
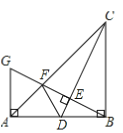
【题目】如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交于点C(0,4).
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,当 MN的值最大时,求△BMN的周长.
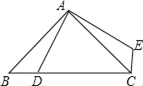
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=4S2,求点P的坐标.

【答案】(1)抛物线的解析式为y=x2﹣5x+4;(2)4+4![]() ;(3)点P的坐标为P(3,﹣2).
;(3)点P的坐标为P(3,﹣2).
【解析】试题(1)利用待定系数法及直线BC上的两点列方程,从而得出一次函数的解析式;根据二次函数上面的两点坐标列出两个方程,从而确定二次函数的一次项系数和常数项;
(2)根据M,N的位置关系,易得他们的横坐标相同,设出对应的坐标,M(x,x2﹣5x+4)(1<x<4),则N(x,﹣x+4),根据两点坐标表示出MN的长度为MN=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x,然后配方,求出MN的最大值;从而△BMN的周长得解;
(3)先求出△ABN的面积为S2,=3,再根据S1=4S2得S1=12.根据平行四边形的底边AB=![]() ,得出平行四边形的高线BD=
,得出平行四边形的高线BD=![]() ,再求x粥上面的BE的长度为3,得点E与点A重合,则过点A平行于BC的直线PQ为y=﹣x+1,最后与二次函数联立方程组,得出点P的坐标.
,再求x粥上面的BE的长度为3,得点E与点A重合,则过点A平行于BC的直线PQ为y=﹣x+1,最后与二次函数联立方程组,得出点P的坐标.
试题解析:
(1)设直线BC的解析式为y=mx+n,
将B(4,0),C(0,4)两点的坐标代入,
得,![]() ,
,
∴![]()
所以直线BC的解析式为y=﹣x+4;
将B(4,0),C(0,4)两点的坐标代入y=x2+bx+c,
得,![]() ,
,
∴![]()
所以抛物线的解析式为y=x2﹣5x+4;
(2)如图1,
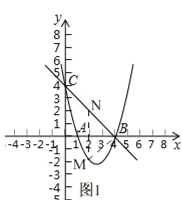
设M(x,x2﹣5x+4)(1<x<4),则N(x,﹣x+4),
∵MN=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,MN有最大值4;
∵MN取得最大值时,x=2,
∴﹣x+4=﹣2+4=2,即N(2,2).
x2﹣5x+4=4﹣5×2+4=﹣2,即M(2,﹣2),
∵B(4.0)
可得BN=2![]() ,BM=2
,BM=2![]()
∴△BMN的周长=4+2![]() +2
+2![]() =4+4
=4+4![]()
(3)令y=0,解方程x2﹣5x+4=0,得x=1或4,
∴A(1,0),B(4,0),
∴AB=4﹣1=3,
∴△ABN的面积S2=×3×2=3,
∴平行四边形CBPQ的面积S1=4S2=12.
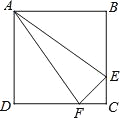
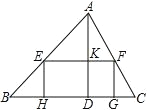
如图2,
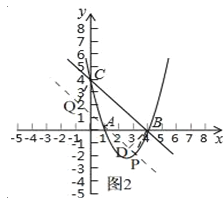
设平行四边形CBPQ的边BC上的高为BD,则BC⊥BD.
∵BC=4![]() ,
,
∴BCBD=12,
∴BD=![]() .
.
过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,连接CQ,则四边形CBPQ为平行四边形.
∵BC⊥BD,∠OBC=45°,
∴∠EBD=45°,
∴△EBD为等腰直角三角形,由勾股定理可得BE=![]() BD=3,
BD=3,
∵B(4,0),
∴E(1,0),
设直线PQ的解析式为y=﹣x+t,
将E(1,0)代入,得﹣1+t=0,解得t=1
∴直线PQ的解析式为y=﹣x+1.
解方程组, ![]() ,
,
得,![]() 或
或![]() ,
,
∵P1(1,0)在x轴上,舍去.
∴点P的坐标为P(3,﹣2).