题目内容
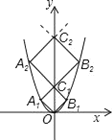
【题目】如图,已知点A1,A2,…,A2019在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2019在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2018A2019C2019B2019都是正方形,则正方形C2018A2019C2019B2019的边长_______.
【答案】![]()
【解析】
根据正方形对角线平分一组对角可得OB1与y轴的夹角为45°,然后表示出OB1的解析式,再与抛物线解析式联立求出点B1的坐标,然后求出OB1的长,再根据正方形的性质求出OC1,表示出C1B2的解析式,与抛物线联立求出B2的坐标,然后求出C1B2的长,再求出C1C2的长,然后表示出C2B3的解析式,与抛物线联立求出B3的坐标,然后求出C2B3的长,从而根据边长的变化规律解答即可.
解:∵四边形OA1C1B1是正方形,
∴OB1与y轴的夹角为45°,
∴OB1的解析式为y=x,
联立![]() ,解得
,解得![]() 或
或![]() ,
,
∴点B1(1,1),
∴OB1=![]() ,
,
∵四边形OA1C1B1是正方形,
∴OC1=![]() ,
,
∵四边形C1A2C2B2是正方形,
∴C1B2与y轴的夹角是45°,
∴C1B2的解析式为y=x+2,
联立![]() ,解得
,解得![]() 或
或![]() ,
,
∴点B2(2,4),
∴C1B2=![]() ,
,
∵四边形C1A2C2B2是正方形,
∴C1C2=![]() ,
,
同理,C2B3的解析式为y=x+4+2=x+6,
联立![]() ,解得
,解得![]() 或
或![]() ,
,
∴点B3(3,9),
∴C2B3=![]() ,
,
……
依此类推,正方形C2018A2019C2019B2019的边长为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目