��Ŀ����
����Ŀ���������¹涨������ͼ��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ����һ�㣬��
����һ�㣬��![]() Ϊ
Ϊ![]() ����һ�㣬����߶�
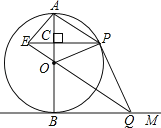
����һ�㣬����߶�![]() �ij��ȴ�����Сֵ���ͳƸ���СֵΪ����ͼ��
�ij��ȴ�����Сֵ���ͳƸ���СֵΪ����ͼ��![]() ��
��![]() ֮��ľ��룮
֮��ľ��룮
��ƽ��ֱ������ϵxOy�У�0Ϊ����ԭ�㣮
��1����![]() ������Ϊ
������Ϊ![]() �����
�����![]() ������
������![]() ֮��ľ���Ϊ______����
֮��ľ���Ϊ______����![]() ������
������![]() ֮��ľ���Ϊ����������
֮��ľ���Ϊ����������
��2�����ֱ��![]() ��˫����
��˫����![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����ô
����ô![]() ____��(����ͼ1�н����о�)
____��(����ͼ1�н����о�)
��3����![]() ������Ϊ
������Ϊ![]() ��������
��������![]() ��ԭ��
��ԭ��![]() ��ʱ����ת
��ʱ����ת![]() ���õ�����
���õ�����![]() ��������ƽ�������к�����
��������ƽ�������к�����![]() ֮��ľ�����ȵĵ�����ɵ�ͼ�μ�Ϊͼ��
֮��ľ�����ȵĵ�����ɵ�ͼ�μ�Ϊͼ��![]() ��
��
������ͼ2�л���ͼ��![]() ��������ͼ��
��������ͼ��![]() ����ɲ��֣�(���漰ƽ����ij������ʱ��������Ӱ��ʾ)
����ɲ��֣�(���漰ƽ����ij������ʱ��������Ӱ��ʾ)
�ڽ�����![]() ��ɵ�ͼ�μ�Ϊͼ��
��ɵ�ͼ�μ�Ϊͼ��![]() ��������
��������![]() ��ͼ��
��ͼ��![]() �Ĺ������ּ�Ϊͼ��
�Ĺ������ּ�Ϊͼ��![]() ����ֱ��д��ͼ��
����ֱ��д��ͼ��![]() ��ͼ��
��ͼ��![]() ֮��ľ��룮
֮��ľ��룮
���𰸡���1��3��5����2��-2����3����ͼ�μ�������ͼ��MΪy��������ᡢ��GOH�ı����ڲ����еĵ㣻��![]()
��������
��1��ֻ������¶��弴�ɽ�����⣻
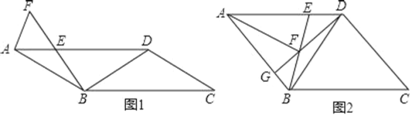
��2������O��ֱ��y=x�Ĵ��ߣ���˫����![]() ���ڵ�A��B������B��BH��x�ᣬ��ͼ1�������¶���ɵ�ֱ��y=x��˫����
���ڵ�A��B������B��BH��x�ᣬ��ͼ1�������¶���ɵ�ֱ��y=x��˫����![]() ֮��ľ�������߶�OB�ij������ֻ�������B�����꣬���ô���ϵ�����Ϳ����k��ֵ��
֮��ľ�������߶�OB�ij������ֻ�������B�����꣬���ô���ϵ�����Ϳ����k��ֵ��
��3���ٹ���O�ֱ�������OE��OF�Ĵ���OG��OH����ͼ2�������¶���ɵ�ͼ��MΪy��������ᡢ��GOH�ı����ڲ����еĵ㣻
����������y=x2-2������OG�Ľ���ΪQ����ͼ3��ͼ��N�ϵ���������Ϊ��x��x2-2���������¶���ɵ�ͼ��W��ͼ��N֮��ľ���Ϊ![]() ����Сֵ����ͨ�������Q������õ�x2�ķ�Χ��Ȼ�����ö��κ��������������x2+��x2-2��2=��x2-
����Сֵ����ͨ�������Q������õ�x2�ķ�Χ��Ȼ�����ö��κ��������������x2+��x2-2��2=��x2-![]() ��2+
��2+![]() ����Сֵ���Ϳɽ�����⣮
����Сֵ���Ϳɽ�����⣮
��1���㣨2��3��������OA֮��ľ���Ϊ3��
�㣨-3��4��������OA֮��ľ���Ϊ![]() ��
��
�ʴ𰸷ֱ�Ϊ��3��5��
��2����ֱ��y=x��˫����![]() ֮��ľ���Ϊ2��
֮��ľ���Ϊ2��
��k��0������ֱ��y=x��˫����![]() �ཻ������֮��ľ���Ϊ0����
�ཻ������֮��ľ���Ϊ0����
����O��ֱ��y=x�Ĵ��ߣ���˫����![]() ���ڵ�A��B������B��BH��x�ᣬ��ͼ1��
���ڵ�A��B������B��BH��x�ᣬ��ͼ1��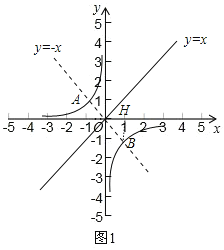
��Rt��OHB����HOB=��HBO=45����OB=2��
����OH=BH=![]() OB=
OB=![]() ��
��
���B������Ϊ(![]() ��
��![]() ����
����
��k=![]()
![]() span>��
span>��
�ʴ�Ϊ��-2��
��3���ٹ���O�ֱ�������OE��OF�Ĵ���OG��OH����ͼ2��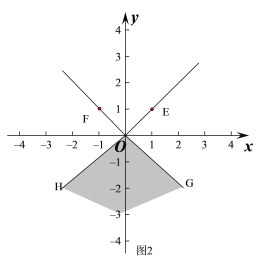
��ͼ��MΪ��y��������ᡢ��GOH�ı����ڲ����еĵ㣨ͼ2�е���Ӱ���֣���
��ͼ��W��ͼ��N֮��ľ���Ϊ
4 |
3 |
��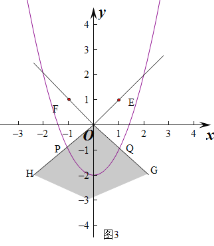
���ɣ���������y=x2-2������OH�Ľ���ΪP��������OG�Ľ���ΪQ����ͼ3��
ͼ��NΪ��������P��Q֮�䣨��P��Q���IJ��֣���ͼ��N�ϵ���������Ϊ��x��x2-2����
��ͼ��W��ͼ��N֮��ľ���Ϊ![]() ����Сֵ��
����Сֵ��
��E�������Ϊ(1��1)
��ֱ��OE�Ľ���ʽΪ��y=x����ֱ��OG�Ľ���ʽΪ��y=-x
����������![]()
��ã�![]() ��
��![]()
�ʵ�Q������Ϊ(1��-1)���Ӷ���0��x2��1��
�ɴ˿ɵ�x2+��x2-2��2=��x2-![]() ��2+
��2+![]() ����СֵΪ��1-
����СֵΪ��1-![]() ��2+
��2+![]() =2��
=2��
��ͼ��W��ͼ��N֮��ľ���Ϊ![]() ��
��