题目内容
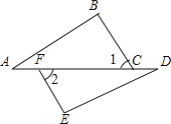
【题目】如图，△ABC和△DEC都是等腰直角三角形，C为它们的公共直角顶点，连AD，BE，F为线段AD的中点，连接CF
（1）如图1，当D点在BC上时，求证：①BE=2CF，②BE⊥CF．
（2）如图2，把△DEC绕C点顺时针旋转一个锐角，其他条件不变，问（1）中的关系是否仍然成立？如果成立请证明．如果不成立，请写出相应的正确的结论并加以证明．
【答案】
（1）
证明：
①∵△ABC和△DEC都是等腰直角三角形，
∴BC=AC，CD=CE，∠ACB=∠ECD=90°，
在△BCE和△ACD中
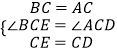
∴△BCE≌△ACD（SAS），
∴BE=AD，∠EBC=∠DAC，
∵F为线段AD的中点，
∴CF=AF=DF= 
AD
∴BE=2CF；
②∵AF=CF，
∴∠DAC=∠FCA，
∵∠BCF+∠ACF=90°，
∴∠BCF+∠EBC=90°，
即BE⊥CF；
（2）
证明：旋转一个锐角后，（1）中的关系依然成立．
证明：如图2，延长CF到M，使FM=FC，连接AM，DM，
又AF=DF，
∴四边形AMDC为平行四边形
∴AM=CD=CE，∠MAC=180°﹣∠ACD，
∠BCE=∠BCA+∠DCE﹣∠ACD=180°﹣∠ACD，
即∠MAC=∠BCE，
在△MAC和△ECB中
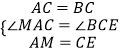
∴△MAC≌△ECB（SAS），
∴CM=BE；∠ACM=∠CBE，
∴BE=CM=2CF；
∴∠CBE+∠BCM=∠ACM+∠BCM=90°，
即BE⊥CF．
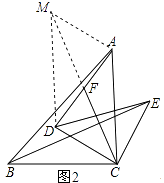
【解析】（1）①由条件可证明Rt△ADC≌Rt△BEC，可证得BE=AD，再利用直角三角形的性质可证明BE=2CF；②由直角三角形的性质可得CF=DF，可证明∠FCD=∠ADC，可证得∠EBC+∠FCD=90°，可证明结论；（2）延长CF到M，使FM=FC，连接AM，DM，可证明四边形ACDM为平行四边形，进一步可证明△MAC≌△ECB，则可得MC=BE，可证得BE=2CF，再结合∠ACB=90°，可证明BE⊥CF．
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案，需要熟知等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°．
