题目内容
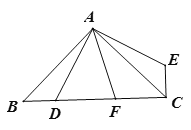
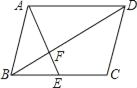
【题目】如图，在平行四边形ABCD中，E是BC的中点，且∠AEC＝∠DCE，则下列结论不正确的是（ ）
A. BF=
DFB. S△AFD＝2S△EFBC. 四边形AECD是等腰梯形D. ∠AEB＝∠ADC
【答案】B
【解析】
根据已知条件即可推出△BEF∽△DAF，推出A项为正确，已知条件可以推出四边形AECD为等腰梯形，推出C项正确，结合平行四边形的性质，可以推出D项正确，所以B项是错误的．
解：∵平行四边形ABCD中，
∴△BEF∽△DAF，
∵E是BC的中点，
∴BF：FD＝BE：AD，
∴BF＝
DF，
故A项正确；
∵∠AEC＝∠DCE，
∴四边形AECD为等腰梯形，
故C项正确；
∵△BEF∽△DAF，BF＝DF，
∴S△AFD＝4S△EFB，
故B项不正确；
∵∠AEB+∠AEC＝180°
∠ADC+∠C＝180°
∠AEC＝∠C
∴∠AEB＝∠ADC
因此D项正确．
故选：B．
练习册系列答案
相关题目
