题目内容
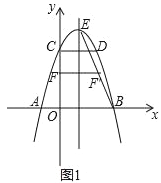
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC,点D在函数图象上,CD∥x轴且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图1,连BE,线段OC上的点F关于直线l的对称点F’恰好在线段BE上,求点F的坐标;
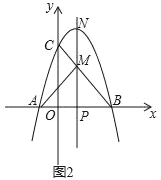
(3)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
【答案】(1)3;(2)点F的坐标为(0,2);(3)存在满足题意的点Q,其坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】试题分析:(1)由条件可求得抛物线对称轴,则可求得b的值;由OB=OC,可用c表示出B点坐标,代入抛物线解析式可求得c的值;
(2)可设F(0,m),则可表示出F′的坐标,由B、E的坐标可求得直线BE的解析式,把F′坐标代入直线BE解析式可得到关于m的方程,可求得F点的坐标;
(3)设点P坐标为(n,0),可表示出PA、PB、PN的长,作QR⊥PN,垂足为R,则可求得QR的长,用n可表示出Q、R、N的坐标.在Rt△QRN中,由勾股定理可得到关于n的二次函数,利用二次函数的性质可知其取得最小值时n的值,则可求得Q点的坐标.
试题解析:解:(1)∵CD∥x轴,CD=2,∴抛物线对称轴为x=1,∴﹣![]() =1,b=2.
=1,b=2.
∵OB=OC,C(0,c),∴B点的坐标为(﹣c,0),∴0=﹣c2+2c+c,解得:c=3或c=0(舍去),∴c=3;
(2)设点F的坐标为(0,m).∵对称轴为直线x=1,∴点F关于直线l的对称点F的坐标为(2,m).由(1)可知抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,∴E(1,4).∵直线BE经过点B(3,0),E(1,4),∴利用待定系数法可得直线BE的表达式为y=﹣2x+6.
∵点F在BE上,∴m=﹣2×2+6=2,即点F的坐标为(0,2);
(3)存在点Q满足题意.设点P坐标为(n,0),则PA=n+1,PB=PM=3﹣n,PN=﹣n2+2n+3.
作QR⊥PN,垂足为R.∵S△PQN=S△APM,∴![]() (n+1)(3﹣n)=
(n+1)(3﹣n)=![]() (﹣n2+2n+3)QR,∴QR=1.
(﹣n2+2n+3)QR,∴QR=1.
①点Q在直线PN的左侧时,Q点的坐标为(n﹣1,﹣n2+4n),R点的坐标为(n,﹣n2+4n)N点的坐标为(n,﹣n2+2n+3),∴在Rt△QRN中,NQ2=1+(2n﹣3)2,∴n=![]() 时,NQ取最小值1.此时Q点的坐标为(
时,NQ取最小值1.此时Q点的坐标为( ![]() );
);
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2﹣4).
同理,NQ2=1+(2n﹣1)2,∴n=![]() 时,NQ取最小值1.此时Q点的坐标为(
时,NQ取最小值1.此时Q点的坐标为(![]() ).
).
综上可知:存在满足题意的点Q,其坐标为(![]() )或(
)或(![]() ).
).


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】为了促进学生体育锻炼,某校八年级进行了体育测试,为了解女生体育测试情况,从中抽取了若干名女生的体育测试成绩.
a.体育委员小李在整理频数分布表时,不小心污染了统计表:
分组(分) | 频数 | 频数 |
21<x≤22 | 8 | 0.200 |
22<x≤23 | 4 | n |
23<x≤24 | 7 | 0.175 |
24<x≤25 | 3 | 0.075 |
25<x≤26 | 2 | 0.050 |
26<x≤27 | 8 | 0.200 |
27<x≤28 | m | 0.150 |
28<x≤29 | 2 | 0.050 |
合计 |
|
b.根据频数分布表,绘制如下频数分布直方图:
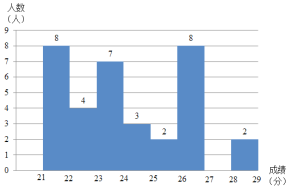
c.在此次测试中,共测试了800米,篮球,仰卧起坐,成绩统计如下:
项目 | 平均分 | 中位数 | 众数 |
800米 | 8.27 | 8.5 | 8.5 |
仰卧起坐 | 7.61 | 8 | 7.5 |
篮球 | 8.69 | 9 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m,n的值;
(2)补全直方图;
(3)请结合C中统计图表,给该校女生体育训练提供建议(至少从两个不同的角度分析).