题目内容
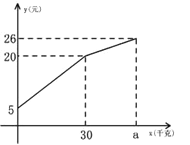
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.
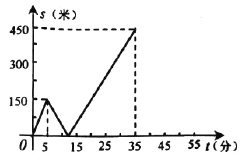
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
【答案】(1)30米/分;(2)见解析;(3)当甲行走30.5分钟或38分钟时,甲、乙两人相距360米.
【解析】
(1)由图象可知t=5时,s=150米,根据速度=路程÷时间,即可解答;
(2)根据图象提供的信息,可知当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500-1050)=450米,甲到达图书馆还需时间;450÷30=15(分),所以35+15=50(分),所以当s=0时,横轴上对应的时间为50.
(3)分别求出当12.5≤t≤35时和当35<t≤50时的函数解析式,根据甲、乙两人相距360米,即s=360,分别求出t的值即可.
(1)甲行走的速度:150÷5=30(米/分);
(2)当t=35时,甲行走的路程为:30×35=1050(米),乙行走的路程为:(35-5)×50=1500(米),
∴当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500-1050)=450米,
∴甲到达图书馆还需时间;450÷30=15(分),
∴35+15=50(分),
∴当s=0时,横轴上对应的时间为50.
补画的图象如图所示(横轴上对应的时间为50),
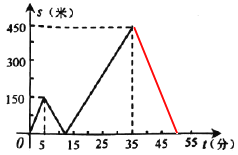
(3)如图,
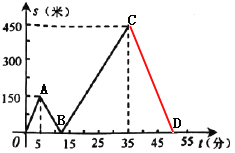
设乙出发经过x分和甲第一次相遇,根据题意得:150+30x=50x,
解得:x=7.5,
7.5+5=12.5(分),
由函数图象可知,当t=12.5时,s=0,
∴点B的坐标为(12.5,0),
当12.5≤t≤35时,设BC的解析式为:s=kt+b,(k≠0),
把C(35,450),B(12.5,0)代入可得:
![]()
解得:![]() ,
,
∴s=20t-250,
当35<t≤50时,设CD的解析式为s=k1x+b1,(k1≠0),
把D(50,0),C(35,450)代入得:
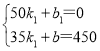
解得: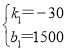
∴s=-30t+1500,
∵甲、乙两人相距360米,即s=360,
解得:t1=30.5,t2=38,
∴当甲行走30.5分钟或38分钟时,甲、乙两人相距360米.

【题目】一张长方形桌子可坐6人,按下图方式讲桌子拼在一起.
 ………
………
① ② ③
(1)观察图形,填写下表:
图形(n) | ② | ③ | …… | n |
坐的人数(人) | …… |
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改为每8张桌子拼成1张大桌子,则共可坐多少人?