Question

【题目】我们规定：平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d，点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D，定义点A到图形G的距离跨度为R=D﹣d．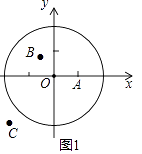
（1）①如图1，在平面直角坐标系xOy中，图形G1为以O为圆心，2为半径的圆，直接写出以下各点到图形G1的距离跨度： A（1，0）的距离跨度；
B（﹣ ， ）的距离跨度；
C（﹣3，﹣2）的距离跨度；
②根据①中的结果，猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是 ．
（2）如图2，在平面直角坐标系xOy中，图形G2为以D（﹣1，0）为圆心，2为半径的圆，直线y=k（x﹣1）上存在到G2的距离跨度为2的点，求k的取值范围．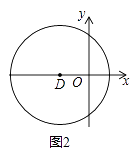
（3）如图3，在平面直角坐标系xOy中，射线OP：y= x（x≥0），⊙E是以3为半径的圆，且圆心E在x轴上运动，若射线OP上存在点到⊙E的距离跨度为2，直接写出圆心E的横坐标xE的取值范围 ．

Answer 1

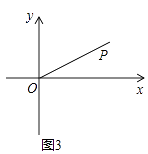
【答案】
（1）2；2；4；圆
（2）解：设直线y=k（x+1）上存在到G2的距离跨度为2的点P（m，k（m+1）），

∴OP= ，

由（1）②知，圆内一点到图形圆的跨度是此点到圆心距离的2倍，圆外一点到图形圆的跨度是此圆的直径，

∵图形G2为以C（1，0）为圆心，2为半径的圆，到G2的距离跨度为2的点，

∴距离跨度小于图形G2的圆的直径4，

∴点P在图形G2⊙C内部，

∴R=2OP=2 ，

∵直线y=k（x+1）上存在到G2的距离跨度为2的点P，

∴2 =2，

∴（k2+1）m2+2（k2﹣1）m+k2=0①，

∵存在点P，

∴方程①有实数根，

∴△=4（k2﹣1）2﹣4×（k2+1）k2=﹣12k2+4≥0，

∴﹣ ≤k≤ ．

（3）﹣1≤xE≤2
【解析】解：（1）①∵图形G1为以O为圆心，2为半径的圆， ∴直径为4，
∵A（1，0），OA=1，
∴点A到⊙O的最小距离d=1，
点A到⊙O的最大距离D=3，
∴点A到图形G1的距离跨度R=D﹣d=3﹣1=2；
∵B（﹣ ， ），
∴OB= =1，
∴点B到⊙O的最小距离d=BG=OG﹣OB=1，
点B到⊙O的最大距离D=BF=FO+OB=2+1=3，
∴点B到图形G1的距离跨度R=D﹣d=3﹣1=2；
∵C（﹣3，﹣2），
∴OC= = ，
∴点C到⊙O的最小距离d=CD=OC﹣OD= ﹣2，
点C到⊙O的最大距离D=CE=OC+OE=2+ ，
∴点C到图形G1的距离跨度R=D﹣d=2+ ﹣（ ﹣2）=4；
所以答案是2，2，4．②a、设⊙O内一点P的坐标为（x，y），
∴OP= ，
∴点P到⊙O的最小距离d=2﹣OP，点P到⊙O的最大距离D=2+OP，
∴点P到图形G1的距离跨度R=D﹣d=2+OP﹣（2﹣OP）=2OP；
∵图形G1的距离跨度为2，
∴2OP=2，
∴OP=1，
∴ =1，
∴x2+y2=1，
即：到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心，1为半径的圆．
b、设⊙O外一点Q的坐标为（x，y），
∴OQ= ，
∴点Q到⊙O的最小距离d=OQ﹣2，点P到⊙O的最大距离D=OQ+2，
∴点P到图形G1的距离跨度R=D﹣d=OQ+2﹣（OQ﹣2）=4；
∵图形G1的距离跨度为2，
∴此种情况不存在，
所以，到图形G1的距离跨度为2的所有的点组成的图形的形状是以点O为圆心，1为半径的圆．
所以答案是：圆；（3）如图，作EC⊥OP于C，交⊙E于D、H．

由题意：⊙E是以3为半径的圆，且圆心E在x轴上运动，若射线OP上存在点到⊙E的距离跨度为2，此时以E为圆心1为半径的圆与射线OP相切，当以E为圆心1为半径的圆与射线OP有交点时，满足条件，
∴CD=2，CH=4，CE=1，
∵射线OP的解析式为y= ，
∴∠COE=30°，OE=2CE=2，
当E′（﹣1，0）时，点O到⊙E的距离跨度为2，
观察图象可知，满足条件的圆心E的横坐标xE的取值范围：﹣1≤xE≤2．
所以答案是：﹣1≤xE≤2．