Question

【题目】在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），其中a为常数，则称点Q是点P的“a级关联点”．例如，点P（1，4）的“3级关联点”为Q（3×1+4，1+3×4），即Q（7，13）．

（1）已知点A（﹣2，6）的“级关联点”是点A1，点B的“2级关联点”是B1（3，3），求点A1和点B的坐标；

（2）已知点M（m﹣1，2m）的“﹣3级关联点”M′位于y轴上，求M′的坐标；

（3）已知点C（﹣1，3），D（4，3），点N（x，y）和它的“n级关联点”N′都位于线段CD上，请直接写出n的取值范围．

Answer 1

【答案】（1）（1，1）（2）（0，﹣16）（3）

【解析】

（1）根据关联点的定义，结合点的坐标即可得出结论；（2）根据关联点的定义和点M（m﹣1，2m）的“﹣3级关联点”M′位于y轴上，即可求出M′的坐标；（3）因为点C（﹣1，3），D（4，3），得到y=3，由点N（x，y）和它的“n级关联点”N′都位于线段CD上，可得到方程组，解答即可．

（1）∵点A（﹣2，6）的“级关联点”是点A1，

∴A1（﹣2×+6，﹣2+×6），

即A1（5，1）．

设点B（x，y），

∵点B的“2级关联点”是B1（3，3），

∴

解得

∴B（1，1）．

（2）∵点M（m﹣1，2m）的“﹣3级关联点”为M′（﹣3（m﹣1）+2m，m﹣1+（﹣3）×2m），

M′位于y轴上，

∴﹣3（m﹣1）+2m=0，

解得：m=3

∴m﹣1+（﹣3）×2m=﹣16，

∴M′（0，﹣16）．

（3）∵点N（x，y）和它的“n级关联点”N′都位于线段CD上，

∴N′（nx+y，x+ny），

∴ ， ，

∴x=3-3n,

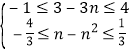∴,解得.