Question

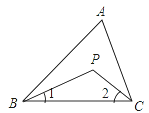
【题目】如图所示，在△ABC中，BP、CP分别是∠ABC和∠ACB的角平分线，∠BPC=134°，求∠A的度数．

Answer 1

【答案】88°．

【解析】

在△BPC中，利用三角形内角和定理先求出∠1+∠2=46°，再根据三角形角平分线的定义可得到∠ABC+∠ACB=2（∠1+∠2）=92°，在△ABC中，再利用三角形内角和定理即可求得∠A的度数.

∵在△BPC中，∠BPC=134°，

∴∠1+∠2=180°﹣∠BPC=180°﹣134°=46°，

∵BP、CP分别是∠ABC和∠ACB的角平分线，

∴∠ABC=2∠1，∠ACB=2∠2，

∴∠ABC+∠ACB=2∠1+2∠2=2（∠1+∠2）=2×46°=92°，

∴在△ABC中，∠A=180°﹣（∠ABC+∠ACB）=180°﹣92°=88°．