题目内容
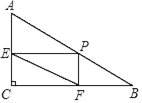
【题目】如图,△ABC是等边三角形,D、E分别是BC、AC上的点,BD=CE,求∠AFE的度数. 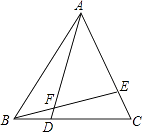
【答案】解;△ABC是等边三角形, ∴AB=BC,∠ABC=∠C=60°.
在△ABD和△BCE中, ,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE.
由三角形弯角的性质得∠AFE=∠BAF+∠ABF,
∠AFE=∠CBE+∠ABF=60°.
【解析】根据等边三角形的性质,可得AB与BC的关系,∠ABC与∠C的关系,根据全等三角形的判定,可得△ABD与△BCE的关系,根据全等三角形的性质,可得∠BAD与∠EBC的关系,根据三角形外角的性质,可得答案.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目