题目内容
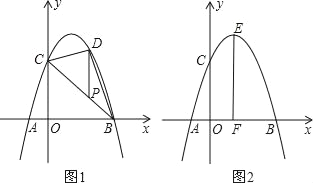
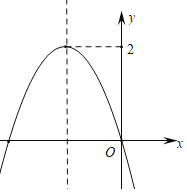
【题目】如图,在平面直角坐标系中,二次函数y=-![]() x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
x2+4的图象与x轴交于A,B两点,与y轴交于点C,⊙C的半径为2,M是⊙C上任意一点,连接MB,取MB的中点D,连接OD,则线段OD的取值范围是______.
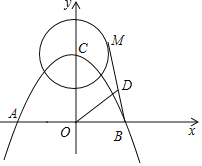
【答案】![]() -1≤OD≤
-1≤OD≤![]() +1
+1
【解析】
连接AM,当点A、C、M共线时,来求AM的最值,结合三角形中位线定理可以求得OD的取值范围.
解:由y=-![]() x2+4得到:A(-2
x2+4得到:A(-2![]() ,0),C(0,4).
,0),C(0,4).
则AC=2![]() .
.
连接AM,如图,
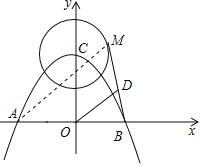
∵D为MB的中点,O为AB的中点,
∴OD为△ABM的中位线,
∴OD=![]() AM.
AM.
当AM的值最小时,OD的值最小.当直线AC经过点M时,AM最小,此时AM=2![]() -2,OD最小值=
-2,OD最小值=![]() AM=
AM=![]() -1.
-1.
当AM的值最大时,OD的值最大,当线段AC延长线经过点M时,AM最大,此时AM=2![]() +2,OD最小值=
+2,OD最小值=![]() AM=
AM=![]() +1.
+1.
所以线段OD的取值范围是![]() -1≤OD≤
-1≤OD≤![]() +1.
+1.
故答案是:![]() -1≤OD≤
-1≤OD≤![]() +1.
+1.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目