Question

【题目】已知：在△ABC中，AB=6，AC=BC=5，将△ABC绕点A按顺时针方向旋转（旋转角度小于180°），得到△ADE，点B的对应点为点D，点C的对应点为点E．

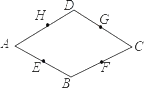
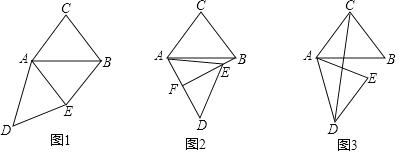
（1）如图1，连接BE，若∠DAB+∠ACB=180°，请判断四边形AEBC的形状，并说明理由；

（2）如图2，设BE的延长线与AD交于点F，若AF=FD，求∠BAD的度数；

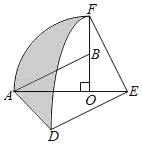
（3）如图3，连接CD，若∠CAE=∠ACB，求CD的长．

Answer 1

【答案】（1）结论：四边形AEBC是菱形，理由见解析；（2）60°；（3）CD=．

【解析】

（1）结论：四边形AEBC是菱形．
（2）如图2中，连接BD．只要证明△ABD是等边三角形即可．
（3）如图3中，在BA的延长线上 取一点D′，使得AD=AD′，连接CD′，作CH⊥AB于H．证明△D′AC≌△DAC可得CD=CD′，利用勾股定理求出CD′即可．

解：（1）结论：四边形AEBC是菱形．

理由：如图1中，

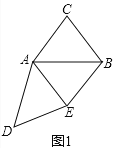
由旋转的性质可知：∠DAB=∠EAC，

∵∠DAB+∠ACB=180°，

∴∠EAC+∠ACB=180°，

∴AE∥BC，

∵AE=BC，

∴四边形AEBC是平行四边形，

∵AE=AC，

∴四边形AEBC是菱形．

（2）如图2中，连接BD．

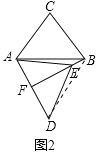
∵AE=DE，AF=DF，

∴EF垂直平分线段AD，

∴BA=BD，

∵AB=AD，

∴△ABD是等边三角形，

∴∠BAD=60°．

（3）如图3中，在BA的延长线上取一点D′，使得AD=AD′，连接CD′，作CH⊥AB于H．

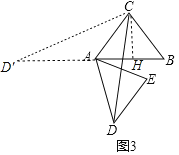
∵∠DAE=∠B，∠CAE=∠ACB

∴D′AC=∠ACB+∠B=∠CAE+∠DAE=∠DAC，

∵AC=AC，

∴△D′AC≌△DAC（SAS）

∴CD=CD′，

易知：CH=4，D′H=9，

由勾股定理得到：CD′==，

∴CD=．