题目内容
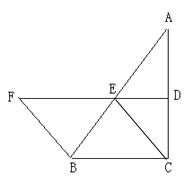
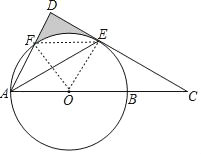
【题目】AB是⊙O的直径,点E是弧BF的中点,连接AF交过E的切线于点D,AB的延长线交该切线于点C,若∠C=30°,⊙O的半径是2,则图形中阴影部分的面积是_____.
【答案】![]()
【解析】
连接OE,OF、EF,根据切线的性质和含30°角的直角三角形的性质求得CE的长,再由已知条件求得AE=CE=![]() ,然后在直角三角形ADE中求得AD和DE,再根据三角形的面积公式和扇形的面积公式求阴影部分的面积即可.
,然后在直角三角形ADE中求得AD和DE,再根据三角形的面积公式和扇形的面积公式求阴影部分的面积即可.
解:连接OE,OF、EF,
∵DE是切线,
∴OE⊥DE,
∵∠C=30°,OB=OE=2,
∴∠EOC=60°,OC=2OE=4,
∴CE=OC×sin60°=4×sin60°=![]() ,
,
∵点E是弧BF的中点,
∴∠EAB=∠DAE=30°,∠DAO=60°,
∴F,E是半圆弧的三等分点,
∴∠EOF=∠EOB=∠AOF=60°,
∴OE∥AD,
∴∠ADC=90°,
∵∠EAB=∠C=30°
∴AE=CE=![]() ,
,
∵∠EAD=30°,∠ADC=90°,
∴DE=![]() ,
,
∴AD=DE×tan60°=![]() ,
,
∴S△ADE=![]()
∵△FOE和△AEF同底等高,
∴△FOE和△AEF面积相等,
∴图中阴影部分的面积为:S△ADE﹣S扇形FOE=![]() .
.
故答案为:![]() .
.

【题目】涌泉镇是中国无核蜜桔之乡,已知某蜜桔种植大户冯大爷的蜜桔成本为2元/千克,如果在未来90天蜜桔的销售单价p(元/千克)与时间t(天)之间的函数关系式为p=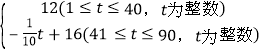 ,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
时间t/天 | 1 | 10 | 20 | 40 | 70 | 90 |
日销售量y/千克 | 105 | 150 | 200 | 300 | 450 | 550 |
(1)求y与t之间的函数表达式;
(2)在未来90天的销售中,预测哪一天的日销售利润最大?最大日销售利润为多少元?
(3)在实际销售的后50天中,冯大爷决定每销售1千克蜜桔就捐赠n元利润(n<5)给留守儿童作为助学金,销售过程中冯大爷发现,恰好从第51天开始,和前一天相比,扣除捐赠后的日销售利润逐日减少,请求出n的取值范围.