题目内容
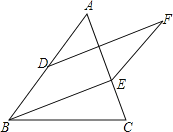
【题目】如图:已知ABCD中,以AB为斜边在ABCD内作等腰直角△ABE,且AE=AD,连接DE,过E作EF⊥DE交AB于F交DC于G,且∠AEF=15°
(1)若EF=![]() ,求AB的长.
,求AB的长.
(2)求证:2GE+EF=AB.
【答案】(1)AB=3;(2)见解析
【解析】
试题分析:(1)作EH⊥AB,交AB于H,根据等腰直角三角形的性质得到∠EAB=∠EBA=45°,EA=EB,于是得到EH=HB=AH=![]() AB,于是得到∠EFH=∠EAB+∠AEF=60°,求得∠FEH=30°,根据直角三角形的性质即可得到结论;
AB,于是得到∠EFH=∠EAB+∠AEF=60°,求得∠FEH=30°,根据直角三角形的性质即可得到结论;
(2)连接EC,根据三角形的内角和得到∠DEA=∠EDA=75°,于是得到∠EAD=30°,求出∠DAB=∠DCB=75°,∠CBA=∠CDA=105°,由于∠ABE=45°,得到∠CBE=60°,推出△BCE是等边三角形,求出∠DCE=15°,CE=BE=AE,推出DG=2GE,证得△AEF≌△ECG,根据全等三角形的性质得到GC=FE,即可得到结论.
解:(1)作EH⊥AB,交AB于H,
∵△ABE是等腰直角三角形,
∴∠EAB=∠EBA=45°,EA=EB,
∴EH=HB=AH=![]() AB,
AB,
∴∠EFH=∠EAB+∠AEF=60°,
∴∠FEH=30°,
∴FH=![]() EF=
EF=![]() EH=
EH=![]() ,
,
∴AB=3,
(2)连接EC,
∵∠AEF=15°,EF⊥DE,AE=AD,
∴∠DEA=∠EDA=75°,
∴∠EAD=30°,
∵∠BAE=45°,
∴∠DAB=∠DCB=75°,∠CBA=∠CDA=105°,
∵∠ABE=45°,
∴∠CBE=60°,
∵AD=BE=BC,
∴△BCE是等边三角形,
∴∠DCE=15°,CE=BE=AE,
∵∠GED=90°,∠GDC=30°,∠DGE=60°,
∴DG=2GE,
∵∠EGC=105°=∠AFE,CE=EF,∠DCE=15°=∠AEF,
在△AEF与△ECG中, ,
,
∴△AEF≌△ECG,
∴GC=FE,
∴AB=DC=DG+GC=2GE+CG=2GE+EF.