题目内容
【题目】如图,折叠边长为![]() 的正方形
的正方形![]() ,使点
,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处(不与点
处(不与点![]() ,
,![]() 重合),点
重合),点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与边
分别与边![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .证明:
.证明:
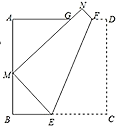
(1)![]() ;
;
(2)若![]() 为
为![]() 中点,则
中点,则![]() ;
;
(3)![]() 的周长为
的周长为![]() .
.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)根据折叠和正方形的性质结合相似三角形的判定定理即可得出答案;
(2)设BE=x,利用勾股定理得出x的值,再利用相似三角形的性质证明即可得出答案;
(3)设BM=x,AM=a-x,利用勾股定理和相似三角形的性质即可得出答案.
证明:(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ,
,
∵![]() 为折痕,
为折痕,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中
中
∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,即
,即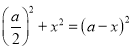 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由(1)知,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(3)设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
由(1)知,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】温州某企业安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲或
件甲或![]() 件乙,甲产品每件可获利
件乙,甲产品每件可获利![]() 元.根据市场需求和生产经验,乙产品每天产量不少于
元.根据市场需求和生产经验,乙产品每天产量不少于![]() 件,当每天生产
件,当每天生产![]() 件时,每件可获利
件时,每件可获利![]() 元, 每增加
元, 每增加![]() 件,当天平均每件利润减少
件,当天平均每件利润减少![]() 元.设每天安排
元.设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | __________ | _____________ |
|
乙 |
|
| _____________ |
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,求每件乙产品可获得的利润.
元,求每件乙产品可获得的利润.