题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 为底边
为底边![]() 上一动点,将射线
上一动点,将射线![]() 绕点
绕点![]() 逆时针旋转后,与射线
逆时针旋转后,与射线![]() 相交于点
相交于点![]() ,且
,且![]()
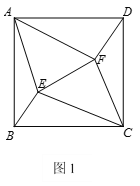
![]() 如图①,当点
如图①,当点![]() 在底边
在底边![]() 上,
上,![]() 时,请直接写出线段
时,请直接写出线段![]() 之间的数量关系;
之间的数量关系;
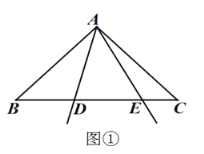
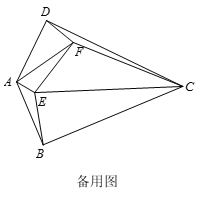
![]() 如图②,当点
如图②,当点![]() 在底边
在底边![]() 上,
上,![]() ,且
,且![]() 时,求证:
时,求证: ![]()
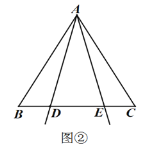
![]() 当
当![]() ,且
,且![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() 或
或![]()
【解析】
(1)在△ABC外取一点F,使AF=AD,CF=BD,连接EF,利用SSS证出△ABD≌△ACF,再证出△ADE≌△AEF,从而证出DE=EF,根据勾股定理和等量代换即可得出结论;
(2)在△ABC外取一点F,使AF=AD,CF=BD,连接EF,作FG⊥BC,交BC延长线于点G,利用SSS证出△ABD≌△ACF,再证出△ADE≌△AEF,从而证出DE=EF,再利用锐角三角函数和勾股定理即可证出结论;
(3)根据点E在线段BC上和BC的延长线上分类讨论,分别画出对应的图形,根据(1)(2)的方法及原理求出CE、EF和CF的关系,从而求出结论.
(1)![]() ,理由如下
,理由如下
在△ABC外取一点F,使AF=AD,CF=BD,连接EF,
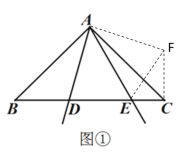
∵AB=AC,∠B=∠ACB=45°
∴△ABD≌△ACF,
∴∠BAD=∠CAF,AD=AF,∠ACF=∠B=45°,
∴∠ECF=∠ACB+∠ACF=90°
∵∠DAE=![]() ∠BAC,
∠BAC,
∴∠BAD+∠CAE=![]() ∠BAC,
∠BAC,
∴∠EAF=∠CAF+∠CAE=![]() ∠BAC,
∠BAC,
∴∠DAE=∠EAF,
∵AD=AF,AE=AE
∴△ADE≌△AEF,
∴DE=EF,
∵![]()
∴![]()
(2)证明:在△ABC外取一点F,使AF=AD,CF=BD,连接EF,作FG⊥BC,交BC延长线于点G,
∵AB=AC,∠B=∠ACB=60°
∴△ABD≌△ACF,
∴∠BAD=∠CAF,AD=AF,∠ACF=∠B=60°,
∵∠DAE=![]() ∠BAC,
∠BAC,
∴∠BAD+∠CAE=![]() ∠BAC,
∠BAC,
∴∠EAF=∠CAF+∠CAE=![]() ∠BAC,
∠BAC,
∴∠DAE=∠EAF,
∵AD=AF,AE=AE
∴△ADE≌△AEF,
∴DE=EF,
又∵∠ECF=60°+60°=120°,
∴∠FCG=60°,
∴CG=FC![]() 60°=
60°=![]() ,
,![]() ,
,
∴在Rt△EFG中,![]() ,
,
∴![]() .
.
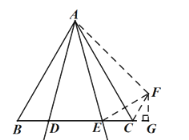
(3)点E线段BC上时,如下图所示,在△ABC外取一点F,使AF=AD,CF=BD,连接EF,
∴CF=BD=2CE
∵AB=AC,∠BAC=120°
∴△ABD≌△ACF, ∠B=∠ACB=30°
∴∠BAD=∠CAF,AD=AF,∠ACF=∠B=30°,
∴∠ECF=∠ACB+∠ACF=60°
∵∠DAE=![]() ∠BAC,
∠BAC,
∴∠BAD+∠CAE=![]() ∠BAC,
∠BAC,
∴∠EAF=∠CAF+∠CAE=![]() ∠BAC,
∠BAC,
∴∠DAE=∠EAF,
∵AD=AF,AE=AE
∴△ADE≌△AEF,
∴DE=EF,
过点F作FE′⊥BC于点E′
∴CE′=CF·cos∠ECF=2CE·![]() =CE
=CE
∴点E′和点E重合
∴DE=EF=CE·tan∠ECF=![]()
∵BD+DE+CE=BC=6
∴2CE+![]() +CE=6
+CE=6
解得:CE=![]() ;
;
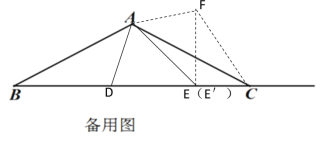
若点E在BC延长线上时,如下图所示,在△ABC外取一点F,使AF=AD,CF=BD,连接EF,过点E作EG⊥FC交FC的延长线于G,设CE=x
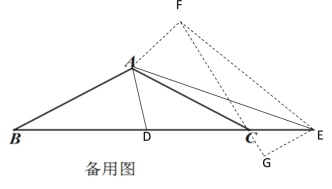
∴CF=BD=2CE=2x
∵AB=AC,∠BAC=120°
∴△ABD≌△ACF, ∠B=∠ACB=30°
∴∠BAD=∠CAF,AD=AF,∠ACF=∠B=30°,
∴∠ECG=∠FCB=∠ACB+∠ACF=60°
∵∠DAE=![]() ∠BAC,
∠BAC,
∴∠BAC-∠BAD+∠CAE=∠DAE=![]() ∠BAC,
∠BAC,
∴∠BAD-∠CAE=![]() ∠BAC,
∠BAC,
∴∠EAF=∠CAF-∠CAE=![]() ∠BAC,
∠BAC,
∴∠DAE=∠EAF,
∵AD=AF,AE=AE
∴△ADE≌△AEF,
∴DE=EF,
在Rt△ECG中,CG=CE·cos∠ECG =![]() x,EG= CE·sin∠ECG =
x,EG= CE·sin∠ECG =![]() x
x
∴FG=CF+CG=![]() x
x
根据勾股定理:EF=![]()
∴DE=EF=![]()
∵BD+DE-CE=BC=6
∴2x+![]() -x=6
-x=6
解得:x=![]()
即CE=![]()
综上:![]() 或
或![]() .
.