题目内容
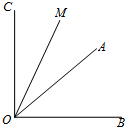 已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
分析:(1)分射线OA在∠BOD的外部和内部两种情况作出图形;
(2)根据互为余角和补角的定义求出∠AOC和∠BOD的度数,再根据角平分线的定义可得∠MOA=
∠AOC,∠BON=
∠BOD,然后根据图形,分∠MON=∠MOA+∠AOB+∠BON和∠MON=∠NOB-∠MOA-∠AOB分别代入数据进行计算即可得解;
(3)分射线OA在∠BOD的外部和内部两种情况解答.
(2)根据互为余角和补角的定义求出∠AOC和∠BOD的度数,再根据角平分线的定义可得∠MOA=
| 1 |
| 2 |
| 1 |
| 2 |
(3)分射线OA在∠BOD的外部和内部两种情况解答.
解答:解:(1)如图1,图2所示;
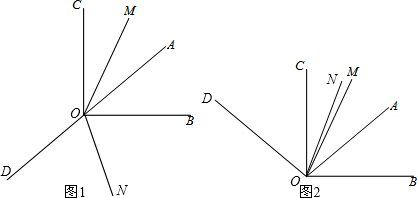
(2)∵∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,
∴∠AOC=90°-∠AOB=50°,∠BOD=180°-∠AOB=140°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOA=
∠AOC=
×50°=25°,∠BON=
∠BOD=
×140°=70°,
①如图1,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°,
②如图2,∠MON=∠NOB-∠MOA-∠AOB=70°-25°-40°=5°,
∴∠MON=135°或5°;
(3)∠MON=α+45°或135°-2α.
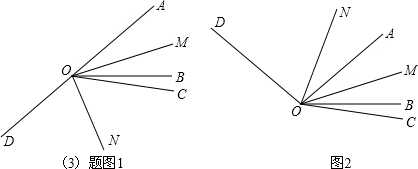

(2)∵∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,
∴∠AOC=90°-∠AOB=50°,∠BOD=180°-∠AOB=140°,
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①如图1,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°,
②如图2,∠MON=∠NOB-∠MOA-∠AOB=70°-25°-40°=5°,
∴∠MON=135°或5°;
(3)∠MON=α+45°或135°-2α.

点评:本题考查了余角和补角,角平分线的定义,难点在于要分情况讨论求解,作出图形更形象直观.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 14、如图,已知∠AOB=30°,M为OB边上一点,以M为圆心、2cm为半径作M.若点⊙M在OB边上运动,则当OM=
14、如图,已知∠AOB=30°,M为OB边上一点,以M为圆心、2cm为半径作M.若点⊙M在OB边上运动,则当OM=
 如图,在平面直角坐标系中,已知△AOB,A(0,-3),B(-2,0).将△OAB先绕点B 逆时针旋转90°得到△BO1A1,再把所得三角形向上平移2个单位得到△B1A2O2;
如图,在平面直角坐标系中,已知△AOB,A(0,-3),B(-2,0).将△OAB先绕点B 逆时针旋转90°得到△BO1A1,再把所得三角形向上平移2个单位得到△B1A2O2;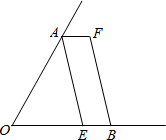 如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,请你只用无刻度的直尺在图中
如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,请你只用无刻度的直尺在图中