��Ŀ����
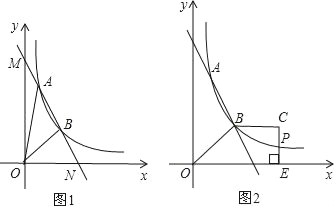
����Ŀ����ͼ1��ֱ��y��k1x+b�뷴��������y��![]() ��ͼ����A��1��6����B��a��3�����㣮
��ͼ����A��1��6����B��a��3�����㣮
��1����k1��k2��ֵ��
��2�����ͼ�Σ��ڵ�һ�����ڣ�ֱ��д��k1x+b��![]() ��0ʱ��x��ȡֵ��Χ��
��0ʱ��x��ȡֵ��Χ��
��3����ͼ2������OBCE�У�BC��OE������C��CE��x���ڵ�E��CE�ͷ�����������ͼ���ڵ�P��������OBCE�����Ϊ9ʱ�����ж�PC��PE�Ĵ�С��ϵ����˵�����ɣ�
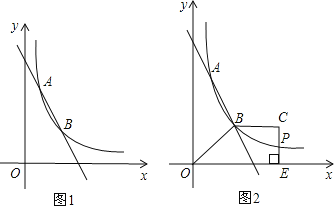
���𰸡���1��k1��k2��ֵ�ֱ�Ϊ��3��6����2��1��x��2ʱ��k1x+b��![]() ��0����3��PC��PE�����ɼ�����.
��0����3��PC��PE�����ɼ�����.
��������
��1���Ȱ�A��1��6������y��![]() �����k2��1��6��6���ٰ�B��a��3������y��
�����k2��1��6��6���ٰ�B��a��3������y��![]() �ɵ�a��2����B������Ϊ��2��3����Ȼ���A��1��6����B��2��3������y��k1x+b�õ�����k1��b�ķ����飬�ⷽ���鼴�ɣ���2���۲�ͼ��õ���x��0��1��x��2ʱ��ֱ��y��k1x+b���ڷ���������y��
�ɵ�a��2����B������Ϊ��2��3����Ȼ���A��1��6����B��2��3������y��k1x+b�õ�����k1��b�ķ����飬�ⷽ���鼴�ɣ���2���۲�ͼ��õ���x��0��1��x��2ʱ��ֱ��y��k1x+b���ڷ���������y��![]() ��ͼ���Ϸ�����k1x+b��
��ͼ���Ϸ�����k1x+b��![]() ��0����3���������ε����ʵõ�BC��OE������B������Ϊ��2��3�����õ�C���������Ϊ3����C������Ϊ��a��3������E������Ϊ��a��0����P��ĺ�����Ϊa������P����y��
��0����3���������ε����ʵõ�BC��OE������B������Ϊ��2��3�����õ�C���������Ϊ3����C������Ϊ��a��3������E������Ϊ��a��0����P��ĺ�����Ϊa������P����y��![]() ��ͼ���ϣ���P������Ϊ��a��
��ͼ���ϣ���P������Ϊ��a��![]() �����������ε������ʽ�õ�
�����������ε������ʽ�õ�![]() ��BC+OE����CE��9����
��BC+OE����CE��9����![]() ��a+a��2����3��9�����a��4����PC��3��
��a+a��2����3��9�����a��4����PC��3��![]() ��PE��
��PE��![]() ��0��
��0��![]() ��������PC��PE��
��������PC��PE��
��1����A��1��6������y��![]() �ã�k2��1��6��6�����Է����������Ľ���ʽΪy��
�ã�k2��1��6��6�����Է����������Ľ���ʽΪy��![]() ��
��
��B��a��3������y��![]() �ã�3��
�ã�3��![]() �����a��2������B������Ϊ��2��3����
�����a��2������B��������2��3����
��A��1��6����B��2��3������y��k1x+b�ã�![]() �����
�����![]() ������k1��k2��ֵ�ֱ�Ϊ��3��6��
������k1��k2��ֵ�ֱ�Ϊ��3��6��
��2��1��x��2ʱ��k1x+b��![]() ��0��
��0��
��3��PC��PE���������£�
���ı���OBDEΪ���Σ�
��BC��OE��
��B��������2��3����
��C���������Ϊ3��
��C��������a��3����
��CE��x�ᣬ
��E������Ϊ��a��0����P��ĺ�����Ϊa��
��P����y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��P��������a��![]() ����
����
������OBCE�����Ϊ9��
��![]() ��BC+OE����CE��9����
��BC+OE����CE��9����![]() ��a+a��2����3��9�����a��4��
��a+a��2����3��9�����a��4��
��C��������4��3����P��������4��![]() ����E��������4��0����
����E��������4��0����
��PC��3��![]() ��
��![]() ��PE��
��PE��![]() ��0��
��0��![]() ��
��
��PC��PE��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�